练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．如图，直线1表示铁路，A、B两点表示某工厂两个生产区，若要在铁路旁修建一个货仓C，使货仓C到两个生产区A，B的距离之和最短，则这样的点C的位置（　　）
    A．有1处B．有2处C．有4处D．不存在

    分析 画出点A关于直线EF的对称点A′，连接A′B交EF于点C，连接AC，由对称的性质可知AC=A′C，由两点之间线段最短可知点C即为所求点．

    解答 解：如图所示：

    画出点A关于直线l的对称点A′，连接A′B交EF于点C，连接AC，
    ∵A、A′关于直线EF对称，
    ∴AC=A′C，
    ∴AC+BC=A′B，
    由两点之间线段最短可知，线段A′B的长即为AC+BC的最小值，故C点即为所求点，
    故选A．

    点评 本题考查的是最短线路问题，熟知对称的性质及两点之间线段最短的知识是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    2．如果单项式6am+2b3与-4.3bna4的和仍是单项式，则-2mn的值为（　　）
    A．6B．-2C．-12D．1

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．如图，在Rt△ABC中，∠ACB=90°，∠ABC=30°，将△ABC绕点C顺时针旋转至△A′B′C，使点A′恰好落在AB上，则旋转角度为（　　）
    A．30°B．45°C．60°D．90°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图，已知DE∥BC，∠ADE=70°，∠C=60°，∠FEC=50°，试说明AB∥EF．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

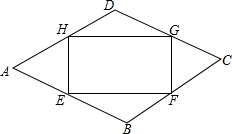    7．某公园要在菱形场地ABCD内划出一个矩形活动场地EFGH，要求矩形的四个顶点E、F、G、H分别在菱形场地的四条边上，且BE=BF=DG=DH菱形的周长为4am，∠ADC=120°．
    （I）如图，设BE=xm，请直接写出矩形EFGH的周长Cm与x之间的函数关系式．并写出自变量的取值范围；
    （2）设矩形的面积为sm2，当BE为多少时，划出的矩形面积最大？请求出最大面积；
    （3）若设计部门从实际需要出发，只需要矩形的面积为$\frac{\sqrt{3}{a}^{2}}{8}$m2就满足需要．能否获得需要的面积？若能，说明理由；若不能．请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．如图是由5个大小相同的正方体搭成的几何体，则从上面看到的形状图是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

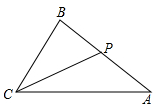    4．如图，在Rt△ABC中，∠ABC=90°，AB=8，BC=6，若动点P从点B开始，按B→A→C→B的路径运动，且速度为每秒2cm，设出发的时间为t秒．求：
    （1）当t为几秒时，CP平分∠ACB？
    （2）当t为何值时，△PBC为等腰三角形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．计算：
    2$\frac{5}{9}$-1$\frac{1}{3}$=
    3$\frac{2}{3}$-1$\frac{1}{6}$+$\frac{2}{3}$=
    6$\frac{2}{3}$×3$\frac{1}{4}$=
    3$\frac{1}{3}$÷$\frac{4}{9}$×1$\frac{1}{3}$=

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．一辆装货的小货车高2.9m，宽为2.4m．要开进下部为长方形，上部为半圆形的某仓库大门（如图），这辆货车能否通过大门？请说明理由．

    查看答案和解析>>

    同步练习册答案