练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．在△ABC中，若AB=AC=10cm，BC=16cm，则这个三角形的重心G到BC的距离是2cm．

    分析 根据等腰三角形的性质得到三角形的重心G在BC边的高，根据勾股定理求出高，根据重心的性质计算即可．

    解答 解：∵AB=AC=10cm，
    ∴△ABC是等腰三角形，
    ∴三角形的重心G在BC边的高，
    设该高为a，
    根据勾股定理，a2+82=102
    则a=6cm，
    根据三角形的重心性质得，G到BC的距离是：6×$\frac{1}{3}$=2cm，
    故答案为：2．

    点评 本题考查的是三角形的重心的概念和性质，三角形的重心是三角形三条中线的交点，且重心到顶点的距离是它到对边中点的距离的2倍．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    2．（1）（-1.7）-2.5
    （2）$\frac{1}{3}$-$\frac{1}{2}$
    （3）-$\frac{1}{6}$-（-$\frac{1}{3}$）
    （4）（-6$\frac{4}{5}$）-（-1.8）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

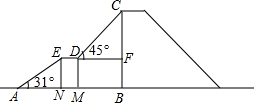    3．如图，是某儿童乐园为小朋友设计的滑梯平面图．已知BC=5米，AB=8米，中间平台宽度DE=1米，EN、DM、CB为三根垂直于AB的支柱，垂足分别为N、M、B，∠EAB=31°，DF⊥BC于F，∠CDF=45°．求DM和BC的水平距离BM的长度．（结果精确到0.1米，参考数据：sin31°≈0.52，cos31°≈0.86，tan31°≈0.60）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．计算：（-$\frac{1}{2}$x2-$\frac{3}{2}$xy+$\frac{1}{4}$y2）•（-2xy2）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．计算：
    （1）（-8）+10+2+（-1）
    （2）-32+16÷（-2）×$\frac{1}{2}$+（-1）2016．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．已知一个三位数，它的百位上的数字为a，十位上的数字为b，个位数字比百位数字小5
    （1）用含字母a、b的多项式表示这个三位数为101a+10b-5
    （2）交换这个三位数的首位和末位数字组成一个新三位数，求原三位数与新三位数的差．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．2012年底某市汽车拥有量为100万辆，而截至2014年底，该市的汽车拥有量已达到144万辆．
    （1）求2012年底至2014年底该市汽车拥有量的年平均增长率；
    （2）该市交通部门为控制汽车拥有量的增长速度，要求到2015年底全市汽车拥有量不超过155.52万辆，预计2015年报废的汽车数量是2014年底汽车拥有量的10%，求2014年底至2015年底该市汽车拥有量的年增长率要控制在什么范围才能达到要求？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．若直线y=kx+b经过A（0，2）和B（3，0）两点，那么这个一次函数关系式是（　　）
    A．y=2x+3B．y=3x+2C．y=-$\frac{2}{3}$x+2D．y=x-1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．如图，AB是⊙O的直径，点C是⊙O上一点，点D是直径AB垂直平分线上一点（C，D在AB的两侧），∠ADB=α．
    （1）如图1，当α=90°，AC=4，BC=2，则CD=3$\sqrt{2}$；
    （2）如图2，当α=60°，AC=4，CD=2$\sqrt{13}$，求BC的长；
    （3）如图3，当α=30°，AB=2，则线段CD的最大值=3+$\sqrt{3}$．

    查看答案和解析>>

    同步练习册答案