
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点三角形ABC(顶点是网格线的交点)
(1)先将△ABC竖直向上平移5个单位,再水平向右平移4个单位得到△A1B1C1,请画出△A1B1C1;
(2)将△A1B1C1绕B1点顺时针旋转90°,得△A2B1C2,请画出△A2B1C2;
(3)求线段B1C1变换到B1C2的过程中扫过区域的面积.

 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】向阳中学数学兴趣小组对关于x的方程(m+1)![]() +(m﹣2)x﹣1=0提出了下列问题:
+(m﹣2)x﹣1=0提出了下列问题:
(1)是否存在m的值,使方程为一元二次方程?若存在,求出m的值,并解此方程;
(2)是否存在m的值,使方程为一元一次方程?若存在,求出m的值,并解此方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(1)班同学为了解2015年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
月均用水量 | 频数(户) | 频率 |
| 6 | 0.12 |
| m | 0.24 |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | n |
| 2 | 0.04 |
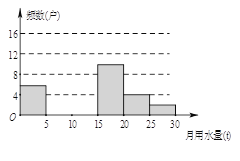
请解答以下问题:
(1)这里采用的调查方式是 (填“普查”或“抽样调查”),样本容量是 ;
(2)填空: ![]() ,
, ![]() ,并把频数分布直方图补充完整;
,并把频数分布直方图补充完整;
(3)若将月均用水量的频数绘成扇形统计图,则月均用水量“
(4)若该小区有1000户家庭,求该小区月均用水量超过10t的家庭大约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是线段AB上一点,△ACD和△BCE都是等边三角形,连结AE,BD,设AE交CD于点F.
(1)求证:△ACE≌△DCB;
(2)求证:△ADF∽△BAD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一工程,在工程招标时,接到甲、乙两个工程队的投标书.施工一天,需付甲工程队工程款1.2万元,乙工程队工程款0.5万元.工程领导小组根据甲、乙两队的投标书测算,有如下方案:①甲队单独完成这项工程刚好如期完成;②乙队单独完成这项工程要比规定日期多用6天;③若甲、乙两队合做3天,余下的工程由乙队单独做也正好如期完成.试问:
(1)两队单独做各要几天完成?
(2)在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡村距城市50km,甲骑自行车从乡村出发进城,出发1小时30分后,乙骑摩托车也从乡村出发进城,结果比甲先到1小时,已知乙的速度是甲的2.5倍,求甲、乙两人的速度。
【答案】甲速12km/h,乙速30km/h.
【解析】试题分析:设甲的速度是![]() 则乙的速度是
则乙的速度是![]() 甲、乙所用时间分别为:
甲、乙所用时间分别为: ![]() 小时、
小时、![]() 小时;根据题意可得甲比乙多用2.5小时,从而可得关于
小时;根据题意可得甲比乙多用2.5小时,从而可得关于![]() 的方程,解方程即可解答此题;注意,最后要结合题意验根.
的方程,解方程即可解答此题;注意,最后要结合题意验根.
试题解析:设甲的速度是![]() 则乙的速度是
则乙的速度是![]() 根据题意列方程,得
根据题意列方程,得
![]() 整理,得
整理,得
![]() ,
,
解得: ![]()
经检验, ![]() 是原方程的解.
是原方程的解.
则![]()
答:甲的速度是12km/h,乙的速度是30km/h.
【题型】解答题
【结束】
24
【题目】已知![]() 求
求![]() 的值 。
的值 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】补全下列各题解题过程.
如图,EF∥AD,∠1 = ∠2,∠BAC = 70°,求 ∠AGD 的度数.

解:∵EF∥AD ( 已知 )
∴∠2 = ( )
又∵∠1=∠2 ( )
∴∠1=∠3 ( )
∴AB∥ ( )
∴∠BAC + = 180°( )
∵∠BAC = 70°(已知 )
∴∠AGD = _ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC的顶点坐标为A(﹣2,3)B(﹣3,1)C(﹣1,2),以坐标原点O为旋转中心,顺时针旋转90°,得到△A′B′C′,点B′、C′分别是点B、C的对应点.
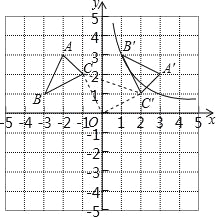
(1)求过点B′的反比例函数解析式;
(2)求线段CC′的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E,F分别是BC,DC上的一个动点,以EF为对称轴折叠△CEF,使点C的对称点G落在AD上,若AB=3,BC=5,则CF的取值范围为 . 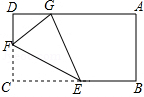
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com