
已知下列 个实数:
个实数:  ,
,  ,
,  ,
, 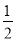 ,
,  ,
,  ,
, 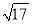 .
.
( )将它们分成有理数和无理数两组.
)将它们分成有理数和无理数两组.
( )将
)将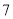 个实数按从小到大的顺序排列,用“
个实数按从小到大的顺序排列,用“ ”号连接.
”号连接.
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源:浙江杭州余杭区2016-2017学年八年级上学期期末数学试卷 题型:填空题
已知:  是
是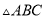 的
的 边上的中线,且
边上的中线,且 .若
.若 ,
,  ,则
,则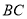 的长为__________.
的长为__________.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度人教版九年级数学下册第26 章同步课时练习:26.1.2 反比例函数的图象和性质 题型:解答题
如图,直线y=2x﹣6与反比例函数 的图象交于点A(4,2),与x轴交于点B.
的图象交于点A(4,2),与x轴交于点B.
(1)求k的值及点B的坐标;
(2)在x轴上是否存在点C,使得AC=AB?若存在,求出点C的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源:人教版2017-2018学年七年级下册5.2《平行线的判定》检测数学试卷 题型:填空题
在同一平面内,不重合的两条直线有_____________种位置关系,它们是___________.
2, 相交或平行. 【解析】试题解析:在同一平面内,不重合的两条直线有2种位置关系,它们是相交或平行.查看答案和解析>>
科目:初中数学 来源:人教版2017-2018学年七年级下册5.2《平行线的判定》检测数学试卷 题型:单选题
如图所示,下列条件中,能判断直线l1∥l2的是( )

A. ∠2=∠1 B. ∠1=∠4 C. ∠2=∠4 D. ∠4+∠2=180°
D 【解析】A.∠1与∠2并不是由直线l1,l2被第三条直线截得的角,所以无法判定l1//l2,此答案错误; B. ∠1与∠4并不是由直线l1,l2被第三条直线截得的角,所以无法判定l1//l2,此答案错误; C.∠2与∠4是由直线l1,l2被第三条直线截得的同旁内角,但是由∠2=∠4不一定得到∠2+∠4=180°,所以无法判定l1//l2,此答案错误; D. ∠2与∠4是...查看答案和解析>>
科目:初中数学 来源:人教版初中数学七年级下册第六章《实数》同步练习 题型:填空题
用“★”定义新运算:对于任意有理数 、
、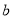 都有
都有 ★
★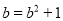 ,例如7★4=
,例如7★4=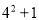 =17,那么
=17,那么 ★(
★( ★2)=__________.
★2)=__________.
查看答案和解析>>
科目:初中数学 来源:人教版初中数学七年级下册第六章《实数》同步练习 题型:单选题
在﹣ ,﹣1,0,3四个数中,最小的数为( )
,﹣1,0,3四个数中,最小的数为( )
A. 0 B. ﹣1 C. ﹣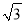 D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源:安徽省太和县2017-2018学年度第一学期期末考试七年级数学试卷 题型:填空题
若点A在数轴上对应的数为2,点B在点A左边,且点B与点A相距7个单位长度,则点B所表示的数是____________.
-5 【解析】∵2?7=?5, ∴点B所表示的数是?5. 故答案为:?5.查看答案和解析>>
科目:初中数学 来源:2017-2018学年七年级数学人教版上册:全册综合测试卷 题型:解答题
解方程:
(1)x- (3x-2)=2(5-x); (2)
(3x-2)=2(5-x); (2) -1=
-1= .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com