
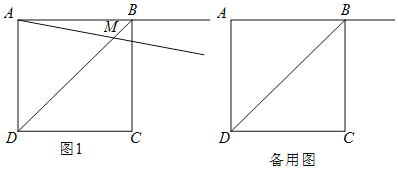
”¾ĢāÄæ”æÕż·½ŠĪABCDµÄ±ß³¤ĪŖ2£¬½«ÉäĻßABČʵćAĖ³Ź±ÕėŠż×Ŗ¦Į£¬ĖłµĆÉäĻßÓėĻ߶ĪBD½»ÓŚµćM£¬×÷CE”ĶAMÓŚµćE£¬µćNÓėµćM¹ŲÓŚÖ±ĻßCE¶Ō³Ę£¬Į¬½ÓCN£®
£Ø1£©ČēĶ¼£¬µ±0”ć£¼¦Į£¼45”揱£ŗ
¢ŁŅĄĢāŅā²¹Č«Ķ¼£»
¢ŚÓƵȏ½±ķŹ¾”ĻNCEÓė”ĻBAMÖ®¼äµÄŹżĮæ¹ŲĻµ£ŗ___________£»
£Ø2£©µ±45”ć£¼¦Į£¼90”揱£¬Ģ½¾æ”ĻNCEÓė”ĻBAMÖ®¼äµÄŹżĮæ¹ŲĻµ²¢¼ÓŅŌÖ¤Ć÷£»
£Ø3£©µ±0”ć£¼¦Į£¼90”揱£¬Čō±ßADµÄÖŠµćĪŖF£¬Ö±½ÓŠ“³öĻ߶ĪEF³¤µÄ×ī“óÖµ£®
”¾“š°ø”æ£Ø1£©¢Ł²¹Ķ¼¼ū½āĪö£»¢Ś”ĻNCE£½2”ĻBAM£»£Ø2£©![]() ”ĻNCE+”ĻBAM£½90”ć£¬Ö¤Ć÷¼ū½āĪö£»£Ø3£©1+
”ĻNCE+”ĻBAM£½90”ć£¬Ö¤Ć÷¼ū½āĪö£»£Ø3£©1+![]() £®
£®
”¾½āĪö”æ
£Ø1£©×÷CE”ĶAMÓŚµćE£¬µćNÓėµćM¹ŲÓŚÖ±ĻßCE¶Ō³Ę£¬Į¬½ÓCN£®ÓÉ”÷ABM”Õ”÷CBM£¬æɵƔĻBAM£½”ĻBCM£¬ÓÉ”ĻABC£½”ĻCEA£½90”ć£¬BC£¬AE½»ÓŚŅ»µć£¬æɵƔĻBAM£½”ĻBCE£¬¼“æɵƵ½”ĻMCE£½2”ĻBAM£¬ÓɵćNÓėµćM¹ŲÓŚÖ±ĻßCE¶Ō³Ę£¬æɵĆCN£½CM£¬¼“æɵƵ½”ĻNCE£½”ĻMCE£¬½ų¶ųµĆ³ö”ĻNCE£½2”ĻBAM£»
£Ø2£©Į¬½ÓCM£¬ÅŠ¶Ø”÷ADM”Õ”÷CDM£¬¼“æɵƵ½”ĻDAM£½”ĻDCM£¬ŌŁøł¾Ż”ĻDAQ£½”ĻECQ£¬¼“æɵƵ½”ĻNCE£½”ĻMCE£½2”ĻDAQ£¬¼“![]() £¬ŌŁøł¾Ż”ĻBAM£½”ĻBCM£¬”ĻBCM+”ĻDCM£½90”ć£¬¼“æɵƵ½
£¬ŌŁøł¾Ż”ĻBAM£½”ĻBCM£¬”ĻBCM+”ĻDCM£½90”ć£¬¼“æɵƵ½![]() £»
£»
£Ø3£©ŅĄ¾Ż”ĻCEA£½90”ć£¬¼“æɵƵ½µćEŌŚŅŌACĪŖÖ±¾¶µÄŌ²ÉĻ£¬µ±EF¾¹żŌ²ŠÄOŹ±£¬¼“æÉµĆ³öĻ߶ĪEF³¤µÄ×ī“óÖµ£®
£Ø1£©¢Ł²¹Č«µÄĶ¼ŠĪČēĶ¼ĖłŹ¾£ŗ
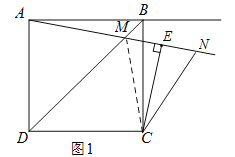
¢Ś”ĻNCE£½2”ĻBAM£®ĄķÓÉČēĻĀ£ŗ
ČēĶ¼1£¬Į¬½ÓMC£®
”ßABCDŹĒÕż·½ŠĪ£¬”ąAB=BC£¬”ĻABM=”ĻCBM£®
”ßBM=BM£¬”ą”÷ABM”Õ”÷CBM£¬”ą”ĻBAM£½”ĻBCM£®
”ß”ĻABC£½”ĻCEA£½90”ć£¬BC£¬AE½»ÓŚŅ»µć£¬”ą”ĻBAM£½”ĻBCE£¬”ą”ĻMCE£½2”ĻBAM£®
”ßµćNÓėµćM¹ŲÓŚÖ±ĻßCE¶Ō³Ę£¬”ąCN£½CM£¬”ą”ĻNCE£½”ĻMCE£¬”ą”ĻNCE£½2”ĻBAM£®
¹Ź“š°øĪŖ£ŗ”ĻNCE£½2”ĻBAM£®
£Ø2£©![]() £®ĄķÓÉČēĻĀ£ŗ
£®ĄķÓÉČēĻĀ£ŗ
ČēĶ¼£¬Į¬½ÓCM£®
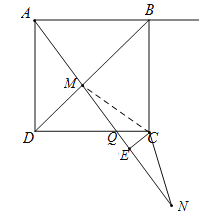
”ßAD£½CD£¬”ĻADM£½”ĻCDM£¬DM£½DM£¬”ą”÷ADM”Õ”÷CDM£¬”ą”ĻDAM£½”ĻDCM£®
”ß”ĻADQ£½”ĻCEQ£½90”ć£¬”ĻAQD£½”ĻCQE£¬”ą”ĻDAQ£½”ĻECQ£¬”ą”ĻNCE£½”ĻMCE£½2”ĻDAQ£¬”ą![]() £®
£®
”ß”ĻBAM£½”ĻBCM£¬”ĻBCM+”ĻDCM£½90”ć£¬”ą![]() £®
£®
£Ø3£©ČēĶ¼£¬”ß”ĻCEA£½90”ć£¬”ąµćEŌŚŅŌACĪŖÖ±¾¶µÄŌ²ÉĻ£¬OĪŖŌ²ŠÄ£¬ÓÉĢāæÉµĆ£ŗOF![]() CD£½1£¬OE£½OC
CD£½1£¬OE£½OC![]() AC
AC![]() £®
£®
”ßOE+OF”ŻEF£¬”ąµ±EF¾¹żŌ²ŠÄOŹ±£¬![]() £®
£®


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÄĻ¾©Ä³ĢŲ²ś×ØĀōµźµÄĻśŹŪijÖÖĢŲ²ś£¬Ęä½ų¼ŪĪŖĆæĒ§æĖ40ŌŖ£¬Čō°“ĆæĒ§æĖ60ŌŖ³öŹŪ£¬ŌņĘ½¾łĆæĢģæÉŹŪ³ö100Ē§æĖ£¬ŗóĄ“¾¹żŹŠ³”µ÷²é·¢ĻÖ£¬µ„¼ŪĆæ½µµĶ3ŌŖ£¬Ę½¾łĆæĢģµÄĻśŹŪĮæŌö¼Ó30Ē§æĖ£¬Čō×ØĀōµźĻśŹŪÕāÖÖĢŲ²śĻėŅŖĘ½¾łĆæĢģ»ńĄū2240ŌŖ£¬ĒŅĻśĮæ¾”æÉÄÜ“ó£¬ŌņĆæĒ§æĖĢŲ²śÓ¦¶Ø¼Ū¶ąÉŁŌŖ?
(1)·½·Ø1:ÉčĆæĒ§æĖĢŲ²śÓ¦½µ¼ŪxŌŖ£¬ÓÉĢāŅā£¬µĆ·½³ĢĪŖ£ŗ___.
·½·Ø2:ÉčĆæĒ§æĖĢŲ²ś½µ¼Ūŗó¶Ø¼ŪĪŖxŌŖ£¬ÓÉĢāŅā£¬µĆ·½³ĢĪŖ£ŗ___.
(2)ĒėÄćŃ”ŌńŅ»ÖÖ·½·ØĶź³É½ā“š.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµxOyÖŠ£¬Ö±Ļßl£ŗy=kx+m½»yÖįÓŚµćC£¬ÓėÅ×ĪļĻßy=ax2+bx½»ÓŚµćA£Ø4£¬0£©”¢B£Ø-![]() £¬-
£¬-![]() £©£®
£©£®
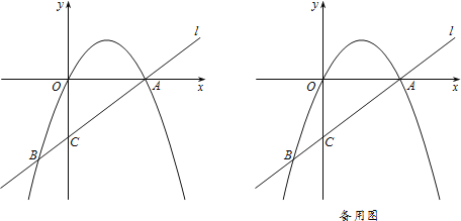
£Ø1£©Ö±ĻßlµÄ±ķ“ļŹ½ĪŖ£ŗ______£¬Å×ĪļĻߵıķ“ļŹ½ĪŖ£ŗ______£»
£Ø2£©ČōµćPŹĒ¶ž“ĪŗÆŹży=ax2+bxŌŚµŚĖÄĻóĻŽÄŚµÄĶ¼ĻóÉĻµÄŅ»µć£¬ĒŅ2S”÷APB=S”÷AOB£¬Ēó”÷AOPµÄĆ껿£»
£Ø3£©ČōµćQŹĒ¶ž“ĪŗÆŹżĶ¼ĻóÉĻŅ»µć£¬ÉčµćQµ½Ö±ĻßlµÄ¾ąĄėĪŖd£¬µ½Å×ĪļĻߵĶŌ³ĘÖįµÄ¾ąĄėĪŖd1£¬µ±|d-d1|=2Ź±£¬ĒėÖ±½ÓŠ“³öµćQµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Õż·½ŠĪABCDµÄ±ßCDŌŚÕż·½ŠĪECGFµÄ±ßCEÉĻ£¬Į¬½ÓDG£¬¹żµćA×÷AH”ĪDG£¬½»BGÓŚµćH£®Į¬½ÓHF£¬AF£¬ĘäÖŠAF½»ECÓŚµćM£®
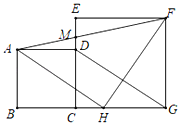
£Ø1£©ĒóÖ¤£ŗ”÷AHFĪŖµČŃüÖ±½ĒČż½ĒŠĪ£®
£Ø2£©ČōAB£½3£¬EC£½5£¬ĒóEMµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¹ŲÓŚxµÄŅ»ŌŖ¶ž“Ī·½³Ģ![]() ÓŠŹµŹżøł£®
ÓŠŹµŹżøł£®
£Ø1£©ĒókµÄȔֵ·¶Ī§£»
£Ø2£©ČōkĪŖÕżÕūŹż£¬ĒŅ·½³ĢÓŠĮ½øö·ĒĮćµÄÕūŹżøł£¬ĒókµÄȔֵ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
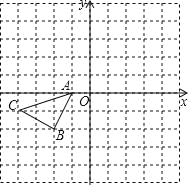
”¾ĢāÄæ”æČēĶ¼£¬·½øńÖ½ÖŠµÄĆæøöŠ”Õż·½ŠĪµÄ±ß³¤¶¼ĪŖ1£¬ŌŚ½ØĮ¢Ę½ĆęÖ±½Ē×ų±źĻµŗ󣬔÷ABCµÄ¶„µć¾łŌŚøńµćÉĻ£®
£Ø1£©ŅŌµćAĪŖŠż×ŖÖŠŠÄ£¬½«”÷ABCČʵćAÄꏱÕėŠż×Ŗ90”ćµĆµ½”÷AB1C1£¬»³ö”÷AB1C1£®
£Ø2£©»³ö”÷ABC¹ŲÓŚŌµćO³ÉÖŠŠÄ¶Ō³ĘµÄ”÷A2B2C2£¬ČōµćCµÄ×ų±źĪŖ£Ø©4£¬©1£©£¬ŌņµćC2µÄ×ų±źĪŖ”” ””£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÄ³Ę·ÅʵēÄŌĻśŹŪ¹«Ė¾ÓŠÓŖĻśŌ±14ČĖ£¬ĻśŹŪ²æĪŖÖʶØÓŖĻśČĖŌ±ŌĀĻśŹŪµēÄŌ¶Ø¶ī£¬Ķ³¼ĘĮĖÕā14ČĖijŌĀµÄĻśŹŪĮæČēĻĀ£Øµ„Ī»£ŗĢØ£©£ŗ
ĻśŹŪĮæ | 200 | 170 | 130 | 80 | 50 | 40 |
ČĖŹż | 1 | 1 | 2 | 5 | 3 | 2 |
£Ø1£©øĆ¹«Ė¾ÓŖĻśŌ±ĻśŹŪøĆĘ·ÅʵēÄŌµÄŌĀĻśŹŪĘ½¾łŹżŹĒ ĢØ£¬ÖŠĪ»ŹżŹĒ ĢØ£¬ÖŚŹżŹĒ ĢØ£®
£Ø2£©ĻśŹŪ²æ¾Ąķ°ŃĆæĪ»ÓŖĻśŌ±ŌĀĻśŹŪĮæ¶ØĪŖ90ĢØ£¬ÄćČĻĪŖŹĒ·ńŗĻĄķ£æĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÖ±½ĒČż½ĒŠĪµÄĶā½ÓŌ²°ė¾¶ĪŖ5£¬ÄŚĒŠŌ²°ė¾¶ĪŖ2£¬Ōņ“ĖČż½ĒŠĪÖܳ¤ĪŖ_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ֊ѧɜĘļµē¶Æ³µÉĻѧµÄĻÖĻóŌ½Ą“Ō½ŹÜµ½Éē»įµÄ¹Ų×¢£®ĪŖ“ĖÄ³Ć½Ģå¼ĒÕߊ”ĄīĖ껜µ÷²éĮĖ³ĒĒųČōøÉĆū֊ѧɜ¼Ņ³¤¶ŌÕāÖÖĻÖĻóµÄĢ¬¶Č£ØĢ¬¶Č·ÖĪŖ£ŗA£ŗĪŽĖłĪ½£»B£ŗ·“¶Ō£»C£ŗŌŽ³É£©²¢½«µ÷Ė½į¹ū»ęÖĘ³ÉĶ¼¢ŁŗĶĶ¼¢ŚµÄĶ³¼ĘĶ¼£Ø²»ĶźÕū£©Ēėøł¾ŻĶ¼ÖŠĢį¹©µÄŠÅĻ¢£¬½ā“šĻĀĮŠĪŹĢā£ŗ
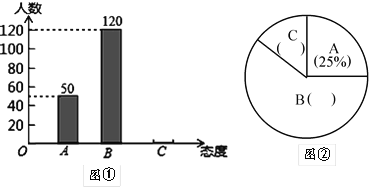
£Ø1£©“Ė“Ī³éŃłµ÷ĖÖŠ£®¹²µ÷ĖĮĖ______Ćū֊ѧɜ¼Ņ³¤£»
£Ø2£©½«Ķ¼ŠĪ¢Ł”¢¢Ś²¹³äĶźÕū£»
£Ø3£©øł¾Ż³éŃłµ÷²é½į¹ū£®ĒėÄć¹Ą¼ĘĪŅŹŠ³ĒĒų80000Ćū֊ѧɜ¼Ņ³¤ÖŠÓŠ¶ąÉŁĆū¼Ņ³¤³Ö·“¶ŌĢ¬¶Č£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com