
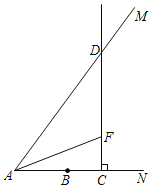
”¾ĢāÄæ”æČēĶ¼£¬ÉäĻßANÉĻÓŠŅ»µćB£¬AB£½5£¬tan”ĻMAN£½![]() £¬µćC“ÓµćA³ö·¢ŅŌĆæĆė3øöµ„Ī»³¤¶ČµÄĖŁ¶ČŃŲÉäĻßANŌĖ¶Æ£¬¹żµćC×÷CD”ĶAN½»ÉäĻßAMÓŚµćD£¬ŌŚÉäĻßCDÉĻČ”µćF£¬Ź¹µĆCF£½CB£¬Į¬½įAF£®ÉčµćCµÄŌĖ¶ÆŹ±¼äŹĒt£ØĆė£©£Øt£¾0£©£®
£¬µćC“ÓµćA³ö·¢ŅŌĆæĆė3øöµ„Ī»³¤¶ČµÄĖŁ¶ČŃŲÉäĻßANŌĖ¶Æ£¬¹żµćC×÷CD”ĶAN½»ÉäĻßAMÓŚµćD£¬ŌŚÉäĻßCDÉĻČ”µćF£¬Ź¹µĆCF£½CB£¬Į¬½įAF£®ÉčµćCµÄŌĖ¶ÆŹ±¼äŹĒt£ØĆė£©£Øt£¾0£©£®
£Ø1£©µ±µćCŌŚµćBÓŅ²ąŹ±£¬ĒóAD”¢DFµÄ³¤£®£ØÓĆŗ¬tµÄ“śŹżŹ½±ķŹ¾£©
£Ø2£©Į¬½įBD£¬Éč”÷BCDµÄĆ껿ĪŖSĘ½·½µ„Ī»£¬ĒóSÓėtÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£®
£Ø3£©µ±”÷AFDŹĒÖį¶Ō³ĘĶ¼ŠĪŹ±£¬Ö±½ÓŠ“³ötµÄÖµ£®
”¾“š°ø”æ£Ø1£©AD£½5t£¬DF=t+5£®£Ø2£©µ±0£¼t£¼![]() Ź±£¬S£½©6t2+10t£®µ±t£¾
Ź±£¬S£½©6t2+10t£®µ±t£¾![]() Ź±£¬S£½6t2©10t£®£Ø3£©tµÄÖµĪŖ
Ź±£¬S£½6t2©10t£®£Ø3£©tµÄÖµĪŖ![]() »ņ
»ņ![]() »ņ
»ņ![]() £®
£®
”¾½āĪö”æ
(1)ĄūÓĆ¹“¹É¶ØĄķĖć³öAD,±ķŹ¾³öCB,¼“æɱķŹ¾³öDF.
(2)·Ö±šĢÖĀŪ0£¼t£¼![]() Ź±ŗĶt£¾
Ź±ŗĶt£¾![]() Ź±,ĄūÓĆĆ껿¹«Ź½¼ĘĖć¼“æÉ.
Ź±,ĄūÓĆĆ껿¹«Ź½¼ĘĖć¼“æÉ.
(3)·Ö±šĢÖĀŪµ±DF£½ADŹ±µÄŅ»ÖÖĒéæö”¢µ±AF£½DFŹ±µÄĮ½ÖÖĒéæö.
½ā£ŗ£Ø1£©ŌŚRt”÷ACDÖŠ£¬AC£½3t£¬tan”ĻMAN£½![]() £¬
£¬
”ąCD£½4t£®
”ąAD£½![]() £¬
£¬
µ±µćCŌŚµćBÓŅ²ąŹ±£¬CB£½3t©5£¬
”ąCF£½CB£®
”ąDF£½4t©£Ø3t©5£©£½t+5£®
£Ø2£©µ±0£¼t£¼![]() Ź±£¬S£½
Ź±£¬S£½![]() £Ø5©3t£©4t£½©6t2+10t£®
£Ø5©3t£©4t£½©6t2+10t£®
µ±t£¾![]() Ź±£¬S£½
Ź±£¬S£½![]() £Ø3t©5£©4t£½6t2©10t£®
£Ø3t©5£©4t£½6t2©10t£®
£Ø3£©¢ŁČēĶ¼1ÖŠ£¬µ±DF£½ADŹ±£¬”÷ADFŹĒÖį¶Ō³ĘĶ¼ŠĪ£®
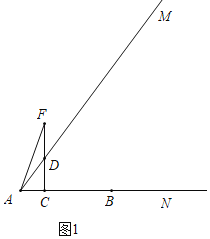
ŌņÓŠ5©3t©4t£½5t£¬½āµĆt£½![]() £¬
£¬
¢ŚČēĶ¼2ÖŠ£¬µ±AF£½DFŹ±£¬”÷ADFŹĒÖį¶Ō³ĘĶ¼ŠĪ£®
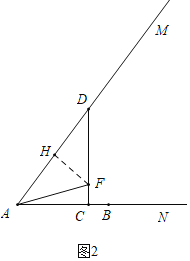
×÷FH”ĶAD£®
”ßFA£½DF£¬
”ąAH£½DH£½![]() t£¬
t£¬
ÓÉcos![]() £¬æɵĆ
£¬æɵĆ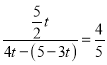 £¬½āµĆt£½
£¬½āµĆt£½![]() £®
£®
¢ŪČēĶ¼3ÖŠ£¬µ±AF£½DFŹ±£¬”÷ADFŹĒÖį¶Ō³ĘĶ¼ŠĪ£®
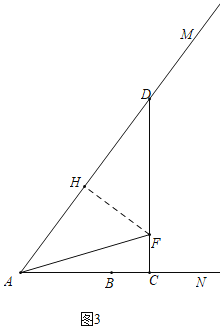
×÷FH”ĶAD£®
”ßFA£½DF£¬
”ąAH£½DH£½![]() t£¬
t£¬
ÓÉcos”ĻFDH£½![]() £¬æɵĆ
£¬æɵĆ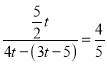 £¬½āµĆt£½
£¬½āµĆt£½![]() £®
£®
×ŪÉĻĖłŹö£¬Āś×ćĢõ¼žµÄtµÄÖµĪŖ![]() »ņ
»ņ![]() »ņ
»ņ![]() £®
£®


 Č«ÓŵćĮ·µ„ŌŖ¼Ę»®ĻµĮŠ“š°ø
Č«ÓŵćĮ·µ„ŌŖ¼Ę»®ĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
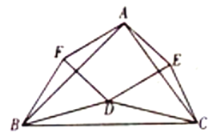
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬µćDŌŚ”÷ABCµÄÄŚ²æĒŅDB=DC£¬µćE£¬FŌŚŌŚ”÷ABCµÄĶā²æ£¬FB=FA£¬EA=EC£¬”ĻFBA=”ĻDBC=”ĻECA.
½ā“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©¢ŁĢīæÕ£ŗ”÷ACE”×_________”×___________£»
¢ŚĒóÖ¤£ŗ”÷CDE”×”÷CBA£»
£Ø2£©Ēó![]() µÄÖµ£»
掙术
£Ø3£©ČōµćDŌŚ”ĻBACµÄĘ½·ÖĻßÉĻ£¬ÅŠ¶ĻĖıߊĪAFDEµÄŠĪד£¬²¢ĖµĆ÷ĄķÓÉ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
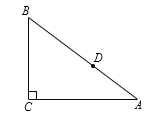
”¾ĢāÄæ”æČēĶ¼£¬Rt”÷ABCÖŠ£¬”ĻC£½90”ć£¬AC£½4£¬BC£½3£¬µćDŹĒAB±ßÉĻŅ»µć£Ø²»ÓėA”¢BÖŲŗĻ£©£¬Čō¹żµćDµÄÖ±Ļß½ŲµĆµÄČż½ĒŠĪÓė”÷ABCĻąĖĘ£¬²¢ĒŅĘ½·Ö”÷ABCµÄÖܳ¤£¬ŌņADµÄ³¤ĪŖ____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ĮāŠĪABCDµÄ±ßABŌŚxÖįÕż°ėÖįÉĻ£¬µćAÓėŌµćÖŲŗĻ£¬µćDµÄ×ų±źŹĒ £Ø3£¬4£©£¬·“±ČĄżŗÆŹży£½![]() £Øk”Ł0£©¾¹żµćC£¬ŌņkµÄÖµĪŖ£Ø””””£©
£Øk”Ł0£©¾¹żµćC£¬ŌņkµÄÖµĪŖ£Ø””””£©
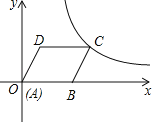
A.12B.15C.20D.32
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßy£½©x2+2x+m+1½»xÖįÓŚµć£Øa£¬0£©ŗĶµć£Øb£¬0£©£¬½»yÖįÓŚµćC£¬Å×ĪļĻ߶„µćĪŖD£¬ĻĀĮŠĖÄøö½įĀŪÖŠ£ŗ¢Łµ±x£¾0Ź±£¬y£¾0£»¢ŚČōa£½©1£¬Ōņb£½3£»¢ŪÅ×ĪļĻßÉĻÓŠĮ½µćP£Øx1£¬y1£©ŗĶQ£Øx2£¬y2£©£¬Čōx1£¼1£¼x2£¬ĒŅx1+x2£¾2£¬Ōņy1£¾y2£»¢ÜµćC¹ŲÓŚÅ×ĪļĻ߶Ō³ĘÖįµÄ¶Ō³ĘµćĪŖE£¬µćG”¢F·Ö±šŌŚxÖįŗĶyÖįÉĻ£¬µ±m£½2Ź±£¬ĖıߊĪEDFGÖܳ¤µÄ×īŠ”ÖµĪŖ6![]() £®ĘäÖŠÕżČ·µÄÓŠ£Ø””””£©øö
£®ĘäÖŠÕżČ·µÄÓŠ£Ø””””£©øö
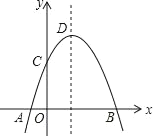
A.0B.1C.2D.3
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ABĪŖ”ŃOµÄÖ±¾¶£¬ACÓė”ŃO½»ÓŚµćF£¬ĻŅADĘ½·Ö”ĻBAC£¬DE”ĶAC£¬“¹×ćĪŖEµć£®

£Ø1£©ĒóÖ¤£ŗDEŹĒ”ŃOµÄĒŠĻߣ»
£Ø2£©Čō”ŃOµÄ°ė¾¶ĪŖ2£¬”ĻBAC£½60”ć£¬ĒóĶ¼ÖŠŅõÓ°²æ·ÖµÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ŗÆŹży£½![]() £Øx£¾0£©µÄĶ¼Ļó¾¹żĮāŠĪOACDµÄ¶„µćDŗĶ±ßACÉĻµÄŅ»µćE£¬ĒŅCE£½2AE£¬ĮāŠĪµÄ±ß³¤ĪŖ8£¬ŌņkµÄÖµĪŖ_____£®
£Øx£¾0£©µÄĶ¼Ļó¾¹żĮāŠĪOACDµÄ¶„µćDŗĶ±ßACÉĻµÄŅ»µćE£¬ĒŅCE£½2AE£¬ĮāŠĪµÄ±ß³¤ĪŖ8£¬ŌņkµÄÖµĪŖ_____£®
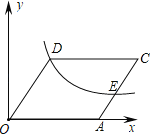
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ“Ó¹²Ļķµ„³µ”¢¹²ĻķĘū³µµČ¹²Ļķ³öŠŠµ½¹²Ļķ³äµē±¦”¢¹²ĻķӟɔµČ¹²ĻķĪļĘ·£¬ø÷Ź½ø÷ŃłµÄ¹²Ļķ¾¼ĆÄ£Ź½ŌŚø÷øöĮģÓņŃøĖŁĘÕ¼°Ó¦ÓĆ£¬Ō½Ą“Ō½¶ąµÄĘóŅµÓėøöČĖ³ÉĪŖ²ĪÓėÕßÓėŹÜŅęÕߣ¬Š”ÓīÉĻĶų²éŌÄĮĖĻą¹Ų׏ĮĻ£¬Ė³±ćŹÕ¼Æµ½ĖÄøö¹²Ļķ¾¼ĆĮģÓņµÄĶ¼±ź£¬²¢½«ĘäÖĘ³É±ąŗÅĪŖA£¬B£¬C£¬DµÄĖÄÕÅæØʬ£Ø³ż±ąŗÅŗĶÄŚČŻĶā£¬ĘäÓąĶźČ«ĻąĶ¬£©£¬½«ÕāĖÄÕÅæØʬ±³Ćę³ÆÉĻ£¬Ļ“ŌČ·ÅŗĆ£®
£Ø1£©“ÓÖŠĖ껜³éČ”Ņ»ÕÅ£¬ĒóøÕŗĆ³éµ½”°¹²Ļķ·žĪń”±µÄøÅĀŹ£®
£Ø2£©“ÓÖŠĖ껜³éČ”Ņ»Õţز»·Å»Ų£©£¬ŌŁ“ÓÖŠĖ껜³éČ”Ņ»ÕÅ£¬ĒėÓĆĮŠ±ķ»ņ»Ź÷דĶ¼µÄ·½·ØĒó³éµ½µÄĮ½ÕÅæØʬĒ”ŗĆŹĒ”°¹²Ļķ³öŠŠ”±ŗĶ”°¹²ĻķÖŖŹ¶”±µÄøÅĀŹ£ØÕāĖÄÕÅæØʬ·Ö±šÓĆĖüĆĒµÄ±ąŗÅA£¬B£¬C£¬D±ķŹ¾£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”抔“ĻŗĶŠ”Ć÷ŃŲĶ¬Ņ»ĢõĀ·Ķ¬Ź±“ÓѧŠ£³ö·¢µ½Ä³³¬ŹŠ¹ŗĪļ£¬Ń§Š£Óė³¬ŹŠµÄĀ·³ĢŹĒ4Ē§Ć×£®Š”“ĻĘļ×ŌŠŠ³µ£¬Š”Ć÷²½ŠŠ£¬µ±Š”“Ļ“ÓŌĀ·»Ųµ½Ń§Š£Ź±£¬Š”Ć÷øÕŗƵ½“ļ³¬ŹŠ£®Ķ¼ÖŠÕŪĻßO©A©B©CŗĶĻ߶ĪOD·Ö±š±ķŹ¾Į½ČĖĄėѧŠ£µÄĀ·³Ģs£ØĒ§Ć×£©ÓėĖł¾¹żµÄŹ±¼ät£Ø·ÖÖÓ£©Ö®¼äµÄŗÆŹż¹ŲĻµ£¬Ēėøł¾ŻĶ¼Ļó»Ų“šĻĀĮŠĪŹĢā£ŗ
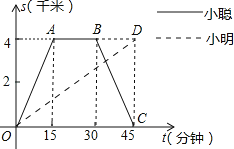
£Ø1£©Š”“ĻŌŚ³¬ŹŠ¹ŗĪļµÄŹ±¼äĪŖ”” ””·ÖÖÓ£¬Š”“Ļ·µ»ŲѧŠ£µÄĖŁ¶ČĪŖ”” ”” Ē§Ć×/·ÖÖÓ£»
£Ø2£©ĒėÄćĒó³öŠ”Ć÷ĄėæŖѧŠ£µÄĀ·³Ģs£ØĒ§Ć×£©ÓėĖł¾¹żµÄŹ±¼ät£Ø·ÖÖÓ£©Ö®¼äµÄŗÆŹż¹ŲĻµŹ½£»
£Ø3£©µ±Š”“ĻÓėŠ”Ć÷ÓĆęĻąÓöŹ±£¬ĖūĆĒĄėѧŠ£µÄĀ·³ĢŹĒ¶ąÉŁĒ§Ć×£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com