
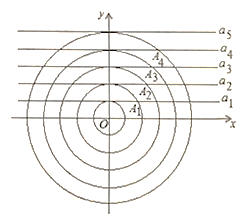
【题目】如图所示,在平面直角坐标系中,一组同心圆的圆心为坐标原点![]() ,它们的半径分别为
,它们的半径分别为![]() .按照“加
.按照“加![]() "依次递增; 一组平行线
"依次递增; 一组平行线![]() , ..分别过
, ..分别过![]() ,且与过该点的圆相切.若半径为
,且与过该点的圆相切.若半径为![]() 的圆与
的圆与![]() 在第一象限内交于点
在第一象限内交于点![]() ,半径为
,半径为![]() 的圆与
的圆与![]() 在第象限内相交于点
在第象限内相交于点![]() ,半径为
,半径为![]() 的圆与
的圆与![]() 在第一象限内相交于点
在第一象限内相交于点![]() 按照此规律,则点
按照此规律,则点![]() 的坐标是( )
的坐标是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知![]() ,
,![]() ,矩形OABC的对角线交于点P,点M在经过点P的函数
,矩形OABC的对角线交于点P,点M在经过点P的函数![]() 的图象上运动,k的值为__________,OM长的最小值__________.
的图象上运动,k的值为__________,OM长的最小值__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 过点
过点![]() ,
,![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
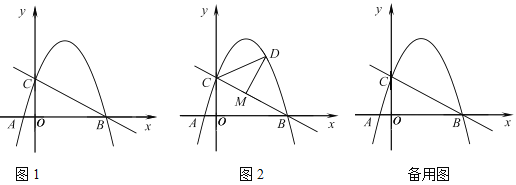
(1)求抛物线的解析式;
(2)在![]() 轴正半轴上存在点
轴正半轴上存在点![]() ,使得
,使得![]() 是等腰三角形,请求出点
是等腰三角形,请求出点![]() 的坐标;
的坐标;
(3)如图2,点![]() 是直线
是直线![]() 上方抛物线上的一个动点.过点
上方抛物线上的一个动点.过点![]() 作
作![]() 于点
于点![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() 中的某个角恰好等于
中的某个角恰好等于![]() 的2倍?若存在,请求出点
的2倍?若存在,请求出点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,
且∠ABM=∠BAM,连接BM,MN,BN.
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
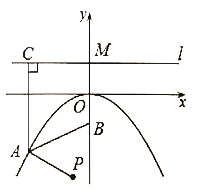
【题目】如图,抛物线![]() 经过点
经过点![]() .点
.点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作直线
作直线![]() 轴,点
轴,点![]() 是抛物线
是抛物线![]() 上一点,
上一点,![]() 于点
于点![]() .
.
![]() 求抛物线解析式:
求抛物线解析式:
![]() 在抛物线对称轴上是否存在一定点
在抛物线对称轴上是否存在一定点![]() ,使得
,使得![]() 永远成立?若存在,求出点
永远成立?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
![]() 若点
若点![]() 坐标为
坐标为![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场要经营一种新上市的文具,进价为![]() 元
元![]() 件.试营销阶段发现:当销售单价是
件.试营销阶段发现:当销售单价是![]() 元时,每天的销售量为
元时,每天的销售量为![]() 件;销售单价每上涨
件;销售单价每上涨![]() 元,每天的销售量就减少
元,每天的销售量就减少![]() 件.
件.
(1)写出商场销售这种文具,每天所得的销售利润![]() (元)与销售单价
(元)与销售单价![]() (元)之间的函数关系式.
(元)之间的函数关系式.
(2)当销售单价定为多少元时,该文具每天的销售利润最大?最大利润为多少元?
(3)商场的营销部结合上述情况,提出了![]() ,
,![]() 两种营销方案:
两种营销方案:
方案![]() :该文具的销售单价高于进价,但不超过
:该文具的销售单价高于进价,但不超过![]() 元;
元;
方案![]() :每天销售量不少于
:每天销售量不少于![]() 件,且每件文具的利润至少为
件,且每件文具的利润至少为![]() 元.
元.
请比较哪种方案的最大利润更高,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作,已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出100千克.
小强:如果以12元/千克的价格销售,那么每天可售出80千克.
小红:通过调查验证,我发现每天的销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元)之间存在一次函数关系.
(元)之间存在一次函数关系.
小强:我发现每天的销售量在70千克至100千克之间.
那么当销售单价为何值时,该超市销售这种水果每天获取的利润为320元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,小聪同学利用直尺和圆规完成了如下操作:
①作∠BAC的平分线AM交BC于点D;
②作边AB的垂直平分线EF,EF与AM相交于点P;
③连接PB,PC.
请你观察图形解答下列问题:
(1)线段PA,PB,PC之间的数量关系是 ;
(2)若∠ABC=70°,求∠BPC的度数.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com