
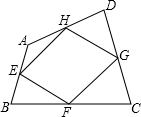
 如图,点E、F、G、H分别为四边形ABCD的四边AB、BC、CD、DA的中点,则关于四边形EFGH,下列说法正确的为( )
如图,点E、F、G、H分别为四边形ABCD的四边AB、BC、CD、DA的中点,则关于四边形EFGH,下列说法正确的为( )| A. | 一定不是平行四边形 | B. | 一定不是中心对称图形 | ||
| C. | 可能是轴对称图形 | D. | 当AC=BD时它是矩形 |
分析 先连接AC,BD,根据EF=HG=$\frac{1}{2}$AC,EH=FG=$\frac{1}{2}$BD,可得四边形EFGH是平行四边形,当AC⊥BD时,∠EFG=90°,此时四边形EFGH是矩形;当AC=BD时,EF=FG=GH=HE,此时四边形EFGH是菱形,据此进行判断即可.
解答 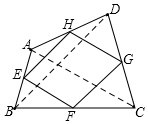 解:连接AC,BD,
解:连接AC,BD,
∵点E、F、G、H分别为四边形ABCD的四边AB、BC、CD、DA的中点,
∴EF=HG=$\frac{1}{2}$AC,EH=FG=$\frac{1}{2}$BD,
∴四边形EFGH是平行四边形,
∴四边形EFGH一定是中心对称图形,
当AC⊥BD时,∠EFG=90°,此时四边形EFGH是矩形,
当AC=BD时,EF=FG=GH=HE,此时四边形EFGH是菱形,
∴四边形EFGH可能是轴对称图形,
故选:C.
点评 本题主要考查了中点四边形的运用,解题时注意:平行四边形是中心对称图形.解决问题的关键是掌握三角形中位线定理.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
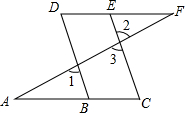 完成下列推理过程
完成下列推理过程查看答案和解析>>
科目:初中数学 来源: 题型:填空题
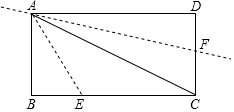 如图,点E,F分别是矩形ABCD的边BC和CD上的点,其中AB=3$\sqrt{2}$,BC=3$\sqrt{6}$,把△ABE沿AE进行折叠,使点B落在对角线AC上,在把△ADF沿AF折叠,使点D落在对角线AC上,点P为直线AF上任意一点,则PE的最小值为2$\sqrt{3}$.
如图,点E,F分别是矩形ABCD的边BC和CD上的点,其中AB=3$\sqrt{2}$,BC=3$\sqrt{6}$,把△ABE沿AE进行折叠,使点B落在对角线AC上,在把△ADF沿AF折叠,使点D落在对角线AC上,点P为直线AF上任意一点,则PE的最小值为2$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com