练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．设n为正整数，且n＜$\sqrt{65}$＜n+1，则n的值为8．

    分析 首先得出$\sqrt{64}$＜$\sqrt{65}$$\sqrt{81}$，进而求出$\sqrt{65}$的取值范围，即可得出n的值．

    解答 解：∵$\sqrt{64}$＜$\sqrt{65}$＜$\sqrt{81}$，
    ∴8＜$\sqrt{65}$＜9，
    ∵n＜$\sqrt{65}$＜n+1，
    ∴n=8，
    故答案为：8．

    点评 此题主要考查了估算无理数，得出$\sqrt{64}$＜$\sqrt{65}$＜$\sqrt{81}$是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    16．记A=$\sum_{k=1}^{2013}$$\sqrt{1+\frac{1}{{k}^{2}}+\frac{1}{（k+1）^{2}}}$，再记[A]表示不超过A的最大整数，则[A]（　　）
    A．2010B．2011C．2012D．2013

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图，字每个小正方形的边长为1个长度单位的长方形网格中，有一个△ABC
    （1）在网格中画出△ABC向下平移3个单位长度得到△A1B1C1；
    （2）在网格中画出△A1B1C1，向右平移4个单位长度得到△A2B2C2；
    （3）如果点A的坐标为（a，b），请写出△A2B2C2各顶点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

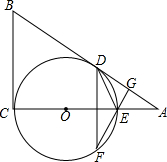    14．如图，已知AB和BC分别与圆O相切于点D、C，AC经过圆心O交圆于点E，AC=2AD且BD=2．
    （1）求：圆O的半径；
    （2）连结DE，作∠FDE=∠ADE交圆于F点，连结FE并延长交AB于点G，设DF=$\sqrt{3}$，求△GDF的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．在正方形ABCD中，点E为直线BC上一点，连接AE，过点E作EF⊥AE交直线AB于点M，交直线CD于点F．
    （1）当点E在线段BC上时，如图①，求证：BE=BM+CF；（提示：过点C作CN∥FM交直线AB的于点N）
    （2）当点E在线段BC的延长线上时，如图②；当点E在线段CB的延长线上时，如图③；线段BE、BM、CF之间又有怎样的数量关系？请直接写出你的猜想，不需要证明；
    （3）若S正方形ABCD=324，sin∠FEC=$\frac{4}{5}$，则MB=32，CF=8或56．

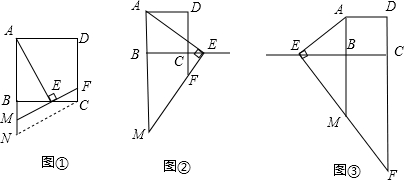
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．下列变形正确的是（　　）
    A．$\sqrt{4\frac{9}{25}}$=$\sqrt{4}$×$\sqrt{\frac{9}{25}}$=2×$\sqrt{\frac{3}{5}}$=$\frac{6}{5}$B．$\sqrt{4{1}^{2}-4{0}^{2}}$=$\sqrt{4{1}^{2}}$-$\sqrt{4{0}^{2}}$=41-40=1
    C．2$\sqrt{3}$×（-5$\sqrt{27}$）=-2×5×$\sqrt{3×27}$=-90D．-3$\sqrt{2}$=$\sqrt{（-3）^{2}×2}$=$\sqrt{18}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．若n为正整数，则$\root{2n+1}{-1}$等于（　　）
    A．-1B．1C．±1D．2n+1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．若使（a-11）2-（4b+112）是完全平方数，求b的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

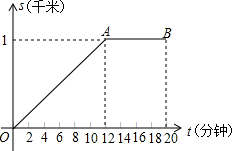    16．小亮早晨从家里出发匀速步行去上学，小亮的妈妈在小亮出发后10分钟，发现小亮的数学课本没带，于是她带上课本立即匀速骑车按小亮上学的路线追赶小亮，结果与小亮同时到达学校．已知小亮在整个上学途中，他出发后t分钟时，他所在的位置与家的距离为s千米，且s与t之间的函数关系的图象如图中的折线段OA-AB所示．
    （1）试求折线段OA-AB所对应的函数关系式；
    （2）请解释图中线段AB的实际意义；
    （3）请在所给的图中画出小亮的妈妈在追赶小亮的过程中，她所在位置与家的距离S（千米）与小亮出发后的时间t（分钟）之间函数关系的图象．（友情提醒：请对画出的图象用数据作适当的标注）

    查看答案和解析>>

    同步练习册答案