
【题目】已知二次函数y=﹣x2+(m﹣2)x+3(m+1)与x轴交于AB两点(A在B左侧),与y轴正半轴交于点C.
(1)当m≠﹣4时,说明这个二次函数的图象与x轴必有两个交点;
(2)若OAOB=6,求点C的坐标;
(3)在(2)的条件下,在x轴下方的抛物线上找一点P,使S△PAC的面积为15,求P点的坐标.
【答案】(1)详见解析;(2)点C的坐标为(0,6);(3)P点的坐标为(﹣5,﹣14)或(2,0).
【解析】
(1)当m≠﹣4时,先得出判别式大于零,再判断出这个二次函数的图象与x轴必有两个交点.
(2)根据抛物线y=﹣x2+(m﹣2)x+3(m+1),求出x1和x2的值,可求OA.
(3)可设P点的坐标为(a,﹣a2﹣a+6),根据S△PAC的面积为15,分P在y轴左边或右边两种情况讨论,列出方程可求P点的坐标.
解:(1)∵m≠﹣4,
∴△=(m﹣2)2﹣4×(﹣1)×3(m+1)=(m+4)2>0,
∴当m≠﹣4时,二次函数y=﹣x2+(m﹣2)x+3(m+1)的图象与x轴必有两个交点;
(2)令y=﹣x2+(m﹣2)x+3(m+1)=0,
解得x1=m+1,x2=﹣3,
∵二次函数y=﹣x2+(m﹣2)x+3(m+1)与x轴交于AB两点(A在B左侧),与y轴正半轴交于点C,
∴A(﹣3,0),B(m+1,0),m+1>0,
∵OAOB=6,
∴3(m+1)=6,
解得m=1,
∴二次函数y=﹣x2﹣x+6,
当x=0时,y=6,
∴点C的坐标为(0,6);
(3)设P点的坐标为(a,﹣a2﹣a+6),
如图一所示,

当P在y轴左边时,![]() ,并且有:
,并且有:![]()
则有:![]()
即:![]() ,
,
解得a=﹣5,a=2(不合题意,舍去),
∴P点的坐标为(﹣5,﹣14);
如图二所示,

当P在y轴右边,![]() ,并且有:
,并且有:![]()
则有:![]()
即:![]() ,
,
解得a=﹣5(不合题意,舍去),a=2,
∴P点的坐标为(2,0);
故P点的坐标为(﹣5,﹣14)或(2,0).


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2-2ax+c与x轴分别交于点A、B(点B在点A的右侧),与y轴交于点C,连接BC,点(![]() ,
,![]() a-3)在抛物线上.
a-3)在抛物线上.
(1)求c的值;
(2)已知点D与C关于原点O对称,作射线BD交抛物线于点E,若BD=DE,①求抛物线所对应的函数表达式 ;②过点B作BF⊥BC交抛物线的对称轴于点F,以点C为圆心,以![]() 的长为半径作⊙C,点T为⊙C上的一个动点,求
的长为半径作⊙C,点T为⊙C上的一个动点,求![]() TB+TF的最小值.
TB+TF的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市计划印制一批宣传册该宣传册每本共![]() 页,由
页,由![]() 两种彩页构成,已知
两种彩页构成,已知![]() 种彩页制版费
种彩页制版费![]() 元/张,
元/张,![]() 种彩页制版费
种彩页制版费![]() 元/张,该宣传册的制版费共计
元/张,该宣传册的制版费共计![]() 元(注:彩页制版费与印数无关)
元(注:彩页制版费与印数无关)
![]() 每本宣传册
每本宣传册![]() 两种彩页各有多少张;
两种彩页各有多少张;
![]() 据了解,
据了解,![]() 种彩页印刷费
种彩页印刷费![]() 元/张,
元/张,![]() 种彩页印刷费
种彩页印刷费![]() 元/张,这批宣传册的制版费与印刷费的和不超过
元/张,这批宣传册的制版费与印刷费的和不超过![]() 元如果按到该市展台处的参观者人手一册发放宣传册,预计最多能发给多少位参观者.
元如果按到该市展台处的参观者人手一册发放宣传册,预计最多能发给多少位参观者.
查看答案和解析>>
科目:初中数学 来源: 题型:
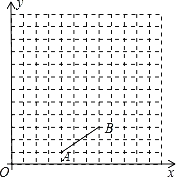
【题目】如图,在平面直角坐标系中,线段AB的端点都在网格线的交点上(每个小方格都是边长为1个单位长度的正方形),按要求完成下列任务.
(1)以点A为旋转中心,将线段AB逆时针旋转90°,得到线段AB1,画出线段AB1;
(2)以原点O为位似中心,将线段AB1在第一象限扩大3倍,得到线段A1B2,画出线段A1B2;(点A,B1的对应点分别是A1,B2)
(3)在线段A1B2上选择一点P,使得以点A,A1,P,B1为顶点的四边形是平行四边形,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据规定,我市将垃圾分为了四类:可回收垃圾、餐厨垃圾、有害垃圾和其他垃圾.现有投放这四类垃圾的垃圾桶各1个,若将用不透明垃圾袋分类打包好的两袋不同垃圾随机投人进两个不同的垃圾桶,投放正确的概率是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是以
是以![]() 为直径的
为直径的![]() 上一点,过点
上一点,过点![]() 作
作![]() 的切线交
的切线交![]() 延长线于点
延长线于点![]() ,取
,取![]() 中点
中点![]() ,连接
,连接![]() 并延长交
并延长交![]() 延长线于点
延长线于点![]() .
.
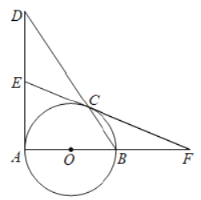
(1)试判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若![]() ,
,![]() ,求
,求![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:对于平面直角坐标系![]() 中的线段
中的线段![]() 和点
和点![]() ,在
,在![]() 中,当
中,当![]() 边上的高为2时,称
边上的高为2时,称![]() 为
为![]() 的“等高点”,称此时
的“等高点”,称此时![]() 为
为![]() 的“等高距离”.
的“等高距离”.
(1)若点![]() 的坐标为(1,2),点
的坐标为(1,2),点![]() 的坐标为(4,2),则在点
的坐标为(4,2),则在点![]() (1,0),
(1,0),![]() (
(![]() ,4),
,4),![]() (0,3)中,
(0,3)中,![]() 的“等高点”是点___;
的“等高点”是点___;
(2)若![]() (0,0),
(0,0),![]() =2,当
=2,当![]() 的“等高点”在
的“等高点”在![]() 轴正半轴上且“等高距离”最小时,点
轴正半轴上且“等高距离”最小时,点![]() 的坐标是__.
的坐标是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB 是⊙O的直径,∠DAB的角平分线AC交⊙O于点C,过点C作CD⊥AD于D,AB的延长线与DC的延长线相交于点P,∠ACB的角平分线CE交AB于点F、交⊙O于E.
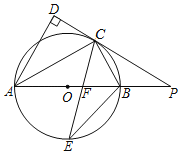
(1)求证:PC与⊙O相切;
(2)求证:PC=PF;
(3)若AC=8,tan∠ABC=![]() ,求线段BE的长.
,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与x轴交于点A,与y轴交于点B,直线
与x轴交于点A,与y轴交于点B,直线![]() 与x轴交于点C.
与x轴交于点C.

(1)求点B的坐标;
(2)横、纵坐标都是整数的点叫做整点.记线段![]() 围成的区域(不含边界)为G.
围成的区域(不含边界)为G.
①当![]() 时,结合函数图象,求区域G内整点的个数;
时,结合函数图象,求区域G内整点的个数;
②若区域G内恰有2个整点,直接写出k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com