
【题目】如图,在正方形网络中,△ABC的三个顶点都在格点上,点A、B、C的坐标分别为(﹣2,4)、(﹣2,0)、(﹣4,1),将△ABC绕原点O旋转180度得到△A1B1C1 . 结合所给的平面直角坐标系解答下列问题: 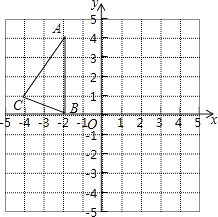
(1)画出△A1B1C1;
(2)画出一个△A2B2C2 , 使它分别与△ABC,△A1B1C1轴对轴(其中点A,B,C与点A2 , B2 , C2对应);
(3)在(2)的条件下,若过点B的直线平分四边形ACC2A2的面积,请直接写出该直线的函数解析式.
 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:
【题目】你认为月球上有水吗?如图是对某中学八年级的140名男生的调查结果.

(1)认为“有水”的频数为________,认为“没有水”的频数是_______,认为“不知道”的频数是_______;
(2)认为“有水”的频率为_______,认为“没有水”的频率是______,认为“不知道”的频率是_______,频率之和为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
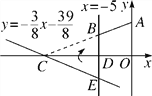
【题目】如图,在平面直角坐标系xOy中,A(0,5),直线x=-5与x轴交于点D,直线y=-![]() x-
x-![]() 与x轴及直线x=-5分别交于点C,E.点B,E关于x轴对称,连接AB.
与x轴及直线x=-5分别交于点C,E.点B,E关于x轴对称,连接AB.
(1)求点C,E的坐标及直线AB的解析式;
(2)若S=S△CDE+S四边形ABDO,求S的值;
(3)在求(2)中S时,嘉琪有个想法:“将△CDE沿x轴翻折到△CDB的位置,而△CDB与四边形ABDO拼接后可看成△AOC,这样求S便转化为直接求△AOC的面积,如此不更快捷吗?”但大家经反复验算,发现S△AOC≠S,请通过计算解释他的想法错在哪里.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某同学在课下设计的一款软件,蓝精灵从点O第一跳落到A1(1,0),第二跳落到A2(1,2),第三跳落到A3(4,2),第四跳落到A4(4,6),第五跳落到A5________,到达A2n后,要向________方向跳________个单位长度落到A2n+1.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=x2+bx+c的图象交x轴于A(﹣1,0)、B(3,0)两点,交y轴于点C,连接BC,动点P以每秒1个单位长度的速度从A向B运动,动点Q以每秒 ![]() 个单位长度的速度从B向C运动,P、Q同时出发,连接PQ,当点Q到达C点时,P、Q同时停止运动,设运动时间为t秒.
个单位长度的速度从B向C运动,P、Q同时出发,连接PQ,当点Q到达C点时,P、Q同时停止运动,设运动时间为t秒.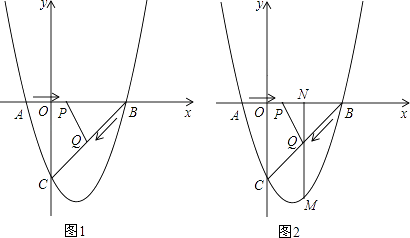
(1)求二次函数的解析式;
(2)如图1,当△BPQ为直角三角形时,求t的值;
(3)如图2,过点Q作QN⊥x轴于N,交抛物线于点M,连结MC,MB,当t为何值时,△MCB的面积最大,并求出此时点M的坐标和△MCB面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
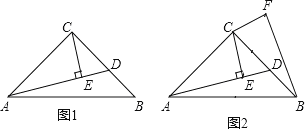
【题目】如图,Rt△ABC中,∠BAC=90°,AB=2,AC=4,D是BC边上一动点,G是BC边上的一动点,GE∥AD分别交AC、BA或其延长线于F、E两点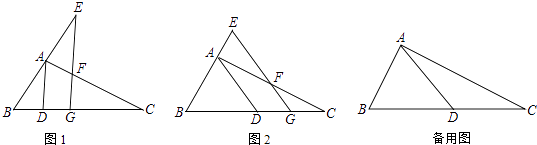
(1)如图1,当BC=5BD时,求证:EG⊥BC;
(2)如图2,当BD=CD时,FG+EG是否发生变化?证明你的结论;
(3)当BD=CD,FG=2EF时,DG的值= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰Rt△ABC中,∠ACB=90°,AC=BC,点D是边BC上任意一点,连接AD,过点C作CE⊥AD于点E.
(1)如图1,若∠BAD=15°,且CE=1,求线段BD的长;
(2)如图2,过点C作CF⊥CE,且CF=CE,连接BF,
求证:AE=BF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com