
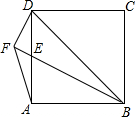
 如图,四边形ABCD是正方形,点E是边AD上一点,DF⊥BE,交BE的延长线于点F,连接AF.若DF=1,AF=$\sqrt{2}$,则BD的长是$\sqrt{10}$.
如图,四边形ABCD是正方形,点E是边AD上一点,DF⊥BE,交BE的延长线于点F,连接AF.若DF=1,AF=$\sqrt{2}$,则BD的长是$\sqrt{10}$. 分析 作DH⊥AF于H,如图,利用正方形的性质得∠ADB=45°,再∴点F、A在以BD为直径的圆上,则利用圆周角定理得到∠AFB=∠ADB=45°,所以∠DFH=45°,于是利用等腰直角三角形的性质得到DH=FH=$\frac{\sqrt{2}}{2}$DF=$\frac{\sqrt{2}}{2}$,然后根据勾股定理可计算出AD=$\sqrt{5}$,于是得到BD=$\sqrt{2}$AD=$\sqrt{10}$.
解答 解:作DH⊥AF于H,如图,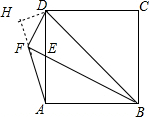
∵四边形ABCD是正方形,
∴∠ADB=45°,
∵DF⊥BE,
∴∠DFB=90°,
而∠BAD=90°,
∴点F、A在以BD为直径的圆上,
∴∠AFB=∠ADB=45°,
∴∠DFH=45°,
∴△DFH为等腰直角三角形,
∴DH=FH=$\frac{\sqrt{2}}{2}$DF=$\frac{\sqrt{2}}{2}$,
∴AH=AF+FH=$\frac{3\sqrt{2}}{2}$,
在Rt△ADH中,AD=$\sqrt{D{H}^{2}+A{H}^{2}}$=$\sqrt{5}$,
∴BD=$\sqrt{2}$AD=$\sqrt{10}$.
故答案为$\sqrt{10}$.
点评 本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质.解决问题的关键是证明∠AFB=45°.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:解答题
 如图,已知△ABC中,AB=AC=20厘米,BC=16厘米,点D为AB的中点.如果点P在线段BC上以6厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.①设点P运动的时间为t,用含有t的代数式表示线段PC的长度;②若点Q的运动速度与点P的运动速度相等,经过t秒后,△BPD与△CQP是否全等,求t的值.
如图,已知△ABC中,AB=AC=20厘米,BC=16厘米,点D为AB的中点.如果点P在线段BC上以6厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.①设点P运动的时间为t,用含有t的代数式表示线段PC的长度;②若点Q的运动速度与点P的运动速度相等,经过t秒后,△BPD与△CQP是否全等,求t的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
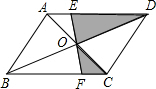 如图,?ABCD的面积是8,对角线AC、DB交于点O,EF过点O分别交AD、BC于E、F,则阴影部分的面积是( )
如图,?ABCD的面积是8,对角线AC、DB交于点O,EF过点O分别交AD、BC于E、F,则阴影部分的面积是( )| A. | 4 | B. | 2 | C. | 6 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 第50行第50列 | B. | 第50行第51列 | C. | 第51行第50列 | D. | 第51行第51列 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
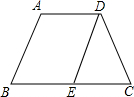 如图,等腰梯形ABCD中,AD∥BC,AD=5,∠B=60°,BC=11,且AB∥DE,△DEC的周长是( )
如图,等腰梯形ABCD中,AD∥BC,AD=5,∠B=60°,BC=11,且AB∥DE,△DEC的周长是( )| A. | 21 | B. | 20 | C. | 19 | D. | 18 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com