
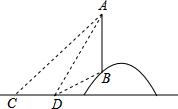
 如图,一电线杆AB立在山坡上,从地面的点C看,测得杆顶端点A的仰角为45°向前走6m到达点D,又测得杆顶端点A和杆底端点B的仰角分别是60°和30°.
如图,一电线杆AB立在山坡上,从地面的点C看,测得杆顶端点A的仰角为45°向前走6m到达点D,又测得杆顶端点A和杆底端点B的仰角分别是60°和30°.分析 (1)延长AB交直线CD于点E,根据直角三角形两锐角互余求得即可;
(2)设AE=x米,在RT△ACE和RT△ADE中,根据三角函数利用x表示出CE和DE,根据CD=CE-DE即可列出方程求得x的值,再在RT△BDE中利用三角函数求得BE的长,则AB的长度即可求解.
解答 解:(1)延长AB交直线CD于点E,
∵∠AED=90°,∠ADE=60°,
∴∠DAB=90°-60°=30°;
(2)设AE=x米.
在RT△CAE中,∠C=45°,
则AE=CE=x米;
∵∠ADE=60°
∴∠DAE=30°
在RT△ADE中,DE=$\frac{\sqrt{3}}{3}$AE=$\frac{\sqrt{3}}{3}$x米,
∵CD=CE-DE=6米,
则x-$\frac{\sqrt{3}}{3}$x=6,
解得:x=9+3$\sqrt{3}$.
则DE=(3$\sqrt{3}$+3)米.
在RT△BDE中,BE=$\frac{\sqrt{3}}{3}$DE=$\frac{\sqrt{3}}{3}$×(3$\sqrt{3}$+3)=(3+$\sqrt{3}$)米.
∴AB=AE-BE=9+3$\sqrt{3}$-(3+$\sqrt{3}$)=6+2$\sqrt{3}$≈9(米).
答:电线杆AB的高度约9米.
点评 此题主要考查了解直角三角形的应用,当两个直角三角形有公共边时,先求出这条公共边的长是解答此类题的一般思路.


科目:初中数学 来源: 题型:选择题
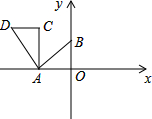 如图,直线y=$\frac{3}{4}$x+3与x轴、y轴分别交于A、B两点,把△AOB绕点A逆时针旋转90°后得到△ACD,则点D的坐标是( )
如图,直线y=$\frac{3}{4}$x+3与x轴、y轴分别交于A、B两点,把△AOB绕点A逆时针旋转90°后得到△ACD,则点D的坐标是( )| A. | (4,3) | B. | (-3,4) | C. | (-7,4) | D. | (-7,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点C在线段AB上,点D是AC的中点,如果CB=$\frac{3}{2}$CD,AB=7cm,那么BC的长为( )
如图,点C在线段AB上,点D是AC的中点,如果CB=$\frac{3}{2}$CD,AB=7cm,那么BC的长为( )| A. | 3cm | B. | 3.5cm | C. | 4cm | D. | 4.5cm |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
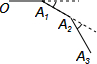 如图,小敏从点0出发,前进10 m到达点A1后,向右转30°前进10m到达点A2,再向
如图,小敏从点0出发,前进10 m到达点A1后,向右转30°前进10m到达点A2,再向查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一个人的体重与他的年龄成正比例关系 | |
| B. | 正方形的面积和它的边长成正比例关系 | |
| C. | 车辆所行驶的路程S一定时,车轮的半径r和车轮旋转的周数m成反比例关系 | |
| D. | 水管每分钟流出的水量Q一定时,流出的总水量y和放水的时间x成反比例关系 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
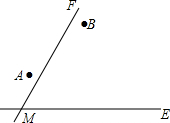 两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部.
两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向的公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
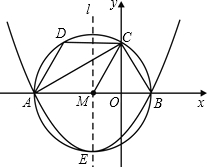 如图,在平面直角坐标系中,四边形ABCD是以AB为直径的⊙M的内接四边形,点A,B在x轴上,△MBC是边长为2的等边三角形,过点M作直线l与x轴垂直,交⊙M于点E,垂足为点M,且点D平分$\widehat{AC}$.
如图,在平面直角坐标系中,四边形ABCD是以AB为直径的⊙M的内接四边形,点A,B在x轴上,△MBC是边长为2的等边三角形,过点M作直线l与x轴垂直,交⊙M于点E,垂足为点M,且点D平分$\widehat{AC}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com