
【题目】如图,在平面直角坐标系中,一次函数图象与x轴,y轴分别交于点A(8,0),B(0,4),点C的坐标为(3,0),动点D是射线BO上一个动点,连结CD,过点C作CD⊥FC,交一次函数图象于点F.
(1)求这个一次函数的解析式;
(2)过点F作FE⊥x轴,垂足为点E,当△OCD与△EFC全等时,求出满足条件的点F的坐标;
(3)点D在运动过程中,是否存在使△ACF是等腰三角形?若存在请求出点F的坐标;不存在,请说明理由.
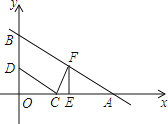
【答案】(1)y=-![]() x+4;(2)(2,3);(3)存在,(0,4)或(8-2
x+4;(2)(2,3);(3)存在,(0,4)或(8-2![]() ,
,![]() )
)
【解析】
(1)利用待定系数法,由点A(8,0),B(0,4)即可求出直线解析式.
(2)△OCD与△EFC全等分为两种情况,由全等得出线段EF或CE长度,进而求出点F的横坐标或纵坐标,代入直线解析式就可以求出点F的坐标.
(3)△ACF是等腰三角形,可以分三种情况讨论,根据等腰三角形性质求出F点的坐标.
(1)设一次函数解析式为y=kx+b(k≠0,k、b为常数),
将点A(8,0),B(0,4)代入得:![]() ,
,
解得:k=-![]() ,b=4.
,b=4.
故一次函数解析式为:y=-![]() x+4.
x+4.
(2)∵△OCD与△EFC全等,
∴可以分两种情况:△OCD≌△EFC或△OCD≌△ECF,
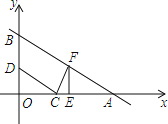
①当△OCD≌△EFC时,
OC=EF=3,
∴点F纵坐标为3,
将y=3代入直线解析式得:x=2,
∴F(2,3).
②当△OCD≌△ECF,
OC=EC=3,
∴点F横坐标为6,
将x=6代入直线解析式得:y=1,
∴F(6,1)(不合题意舍弃).
∴F点坐标为:(2,3)
(3)存在.
△ACF是等腰三角形,
①当CF=AF时,
根据等腰三角形三线合一性质,得点E为AC中点,
AC=5,CE=![]() ,
,
∴OE=![]() ,即F点横坐标为
,即F点横坐标为![]() ,
,
将x=![]() 代入一次函数得y=
代入一次函数得y=![]() ,
,
∴F(![]() ).
).
此时点D会出现在点B的上方,与题意不符,舍去;
②当AF=AC时,OB=4,OA=8,
AB=4![]() .
.
∵EF∥OB,
∴△AEF∽△AOB.
∴![]() ,
,
解得:EF=![]() .
.
将y=![]() 代入直线解析式,得:x=8-2
代入直线解析式,得:x=8-2![]() ,
,
∴F(8-2![]() ,
,![]() ).
).
③当CF=AC=5时,
∵OC=3,OB=4,
∴BC=5,
此时,CB=CF,点F与点B重合,
∴F(0,4) ,
∴点F坐标为:(0,4)或(8-2![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
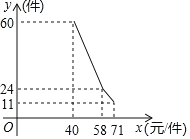
【题目】某店因为经营不善欠下38000元的无息贷款的债务,想转行经营服装专卖店又缺少资金.“中国梦想秀”栏目组决定借给该店30000元资金,并约定利用经营的利润偿还债务(所有债务均不计利息)已知该店代理的某品牌服装的进价为每件40元,该品牌服装日的售量y(件)与销售价x(元/件)之间的关系可用图中的一条折线(实线)来表示.
(1)求日销售量y(件)与销售价x(元/件)之间的函数关系式;
(2)当销售价为多少元时,该店的日销售利润最大;
(3)该店每天支付工资和其它费用共250元,该店能否在一年内还清所有债务.
查看答案和解析>>
科目:初中数学 来源: 题型:
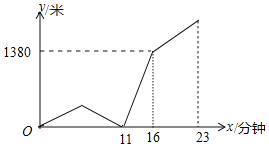
【题目】一天,小明从家出发匀速步行去学校上学.几分钟后,在家休假的爸爸发现小明忘带数学书,于是爸爸立即匀速跑步去追小明,爸爸追上小明后以原速原路跑回家.小明拿到书后以原速的![]() 快步赶往学校,并在从家出发后23分钟到校(小明被爸爸追上时交流时间忽略不计).两人之间相距的路程y(米)与小明从家出发到学校的步行时间x(分钟)之间的函数关系如图所示,则小明家到学校的路程为________米.
快步赶往学校,并在从家出发后23分钟到校(小明被爸爸追上时交流时间忽略不计).两人之间相距的路程y(米)与小明从家出发到学校的步行时间x(分钟)之间的函数关系如图所示,则小明家到学校的路程为________米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(探究)
(1)观察下列算式,并完成填空:
1=12
1+3=4=22;
1+3+5=9=32;
1+3+5+7=16=42;
1+3+5+…+(2n-1)=______.(n是正整数)
(2)如图是某市一广场用正六边形、正方形和正三角形地板砖铺设的图案,图案中央是一块正六边形地板砖,周围是正方形和正三角形的地板砖.从里向外第一层包括6块正方形和6块正三角形地板砖;第二层包括6块正方形和18块正三角形地板砖;以此递推.
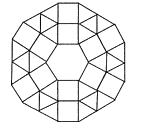
①第3层中分别含有______块正方形和______块正三角形地板砖;
②第n层中含有______块正三角形地板砖(用含n的代数式表示).
(应用)
该市打算在一个新建广场中央,采用如图样式的图案铺设地面,现有1块正六边形、150块正方形和420块正三角形地板砖,问:铺设这样的图案,最多能铺多少层?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2019大洋湾盐城马拉松”的赛事共有三项:A,“全程马拉松”、B,“半程马拉松”、C.“迷你健身跑”,小明和小刚参与了该项赛事的志愿者服务工作,组委会随机将志愿者分配到三个项目组.
(1)小明被分配到“迷你健身跑”项目组的概率为 ;
(2)求小明和小刚被分配到不同项目组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,对于两个点
中,对于两个点![]() ,
,![]() 和图形
和图形![]() ,如果在图形
,如果在图形![]() 上存在点
上存在点![]() ,
,![]() (
(![]() ,
,![]() 可以重合)使得
可以重合)使得![]() ,那么称点
,那么称点![]() 与点
与点![]() 是图形
是图形![]() 的一对平衡点.
的一对平衡点.
(1)如图1,已知点![]() ,
,![]() ;
;
①设点![]() 与线段
与线段![]() 上一点的距离为
上一点的距离为![]() ,则
,则![]() 的最小值是 ,最大值是 ;
的最小值是 ,最大值是 ;
②在![]() ,
,![]() ,
,![]() 这三个点中,与点
这三个点中,与点![]() 是线段
是线段![]() 的一对平衡点的是 ;
的一对平衡点的是 ;
(2)如图2,已知![]() 的半径为1,点
的半径为1,点![]() 的坐标为
的坐标为![]() 在第一象限,且点
在第一象限,且点![]() 与点
与点![]() 是
是![]() 的一对平衡点,求
的一对平衡点,求![]() 的取值范围;
的取值范围;
(3)如图3,已知点![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 长为半径画弧交
长为半径画弧交![]() 的正半轴于点
的正半轴于点![]() .点
.点![]() (其中
(其中![]() )是坐标平面内一个动点,且
)是坐标平面内一个动点,且![]() ,
,![]() 是以点
是以点![]() 为圆心,半径为2的圆,若
为圆心,半径为2的圆,若![]() 上的任意两个点都是
上的任意两个点都是![]() 的一对平衡点,直接写出
的一对平衡点,直接写出![]() 的取值范围.
的取值范围.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育李老师为了解九年级女生体质健康的变化情况,本学期从九年级全体90名女生中随机抽取15名女生进行体质测试,并调取该15名女生上学期的体质测试成绩进行对比,李老师对两次数据(成绩)进行整理、描述和分析.下面给出了部分信息.
![]() .两次测试成绩(百分制)的频数分布直方图如下(数据分组:
.两次测试成绩(百分制)的频数分布直方图如下(数据分组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() );
);
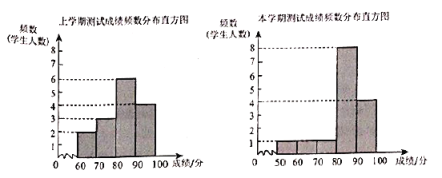
![]() .上学期测试成绩在
.上学期测试成绩在![]() 的是:80 81 83 84 84 88
的是:80 81 83 84 84 88
![]() .两个学期测试成绩的平均数、中位数、众数如下:
.两个学期测试成绩的平均数、中位数、众数如下:
学期 | 平均数 | 中位数 | 众数 |
上学期 | 82.9 |
| 84 |
本学期 | 83 | 86 | 86 |
根据以上信息,回答下列问题:
(1)表中![]() 的值是______;
的值是______;
(2)体育李老师计划根据本学期统计数据安排80分以下(不含80分)的同学参加体质加强训练项目,则九年级约有______名女生参加此项目;
(3)分析这15名女生从上学期到本学期体质健康变化的总体情况.(从两个方面进行分析)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明为今年将要参加中考的好友小李制作了一个(如图)正方体礼品盒,六面上各有一字,连起来就是“预祝中考成功”,其中“预”的对面是“中”,“成”的对面是“功”,则它的平面展开图可能是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知某写字楼AB的正前方有一座信号塔DE,在高为60m的楼顶B处,测得塔尖E处的仰角为30°,从楼底A处向信号塔方向走30m到达C处,测得塔尖E处的仰角为68°,已知点D,C,A在同一水平线上,求信号塔DE的高度.(结果精确到0.1m.参考数据:sin68°≈0.9,cos68°≈0.4,tan 68°≈2.5,![]() ≈1.7).
≈1.7).
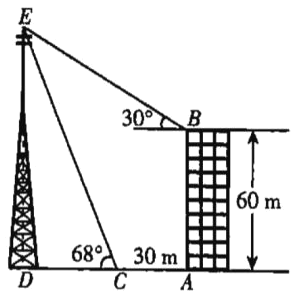
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com