
分析 (1)先把二次根式化为最简二次根式.然后合并即可;
(2)先把二次根式化为最简二次根式.然后进行二次根式的除法运算,再合并即可;
(3)利用完全平方公式和平方差公式计算;
(4)先变形为(x+1)2=16,然后利用直接开平方法解方程.
解答 解:(1)原式=6$\sqrt{5}$-3$\sqrt{5}$+$\frac{\sqrt{5}}{5}$
=$\frac{16\sqrt{5}}{5}$;
(2)原式=$\frac{4\sqrt{3}-5\sqrt{3}}{\sqrt{3}}$+3
=-1+3
=2;
(3)原式=3-2$\sqrt{3}$+1-(9-8)
=4-2$\sqrt{3}$-1
=3-2$\sqrt{3}$;
(4)(x+1)2=16,
x+1=±4,
所以x1=3,x2=-5.
点评 本题考查了解一元二次方程-直接开平方法:形如x2=p或(nx+m)2=p(p≥0)的一元二次方程可采用直接开平方的方法解一元二次方程.也考查了二次根式的混合运算.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
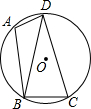 如图,已知四边形ABCD内接于圆O,∠A=105°,BD=CD.
如图,已知四边形ABCD内接于圆O,∠A=105°,BD=CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
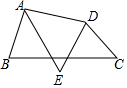 如图,四边形ABCD中,AE平分∠BAD,DE平分∠ADC.
如图,四边形ABCD中,AE平分∠BAD,DE平分∠ADC.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
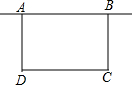 如图,某居民小区要在一块一边靠墙(墙足够长)的高地上修建一个矩形花园ABCD,花园的一边靠墙,另外三边用总长为42m的栅栏围成,CD上留2米的位置做大门.则CD=22 米时,花园的面积最大,最大面积是242平方米.
如图,某居民小区要在一块一边靠墙(墙足够长)的高地上修建一个矩形花园ABCD,花园的一边靠墙,另外三边用总长为42m的栅栏围成,CD上留2米的位置做大门.则CD=22 米时,花园的面积最大,最大面积是242平方米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{13}{54}$ | B. | $\frac{1}{4}$ | C. | 1 | D. | $\frac{1}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,网格中每个小正方形的边长均为1,线段AB、线段EF的端点均在小正方形的顶点上.
如图,网格中每个小正方形的边长均为1,线段AB、线段EF的端点均在小正方形的顶点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com