
【题目】(1)计算:﹣12+(π﹣3.14)0﹣(﹣![]() )﹣2+
)﹣2+![]() ;
;
(2)先化简,再求值:[(2x+y)(2x﹣y)+(x+y)2﹣2(2x2﹣xy)]÷(﹣![]() x),其中x、y满足
x),其中x、y满足![]() +(y+4)2=0.
+(y+4)2=0.
【答案】(1)﹣3;(2)﹣2x﹣8y,22
【解析】
(1)根据零指数幂、负整数指数幂可以解答本题;
(2)根据平方差公式、完全平方公式和多项式除以单项式可以化简题目中的式子,再根据![]() +(y+4)2=0,可以得到x、y的值,然后将x、y代入化简后的式子即可解答本题.
+(y+4)2=0,可以得到x、y的值,然后将x、y代入化简后的式子即可解答本题.
解:(1)﹣12+(π﹣3.14)0﹣(﹣![]() )﹣2+
)﹣2+![]()
=﹣1+1﹣9+6
=﹣3;
(2)[(2x+y)(2x﹣y)+(x+y)2﹣2(2x2﹣xy)]÷(﹣![]() x)
x)
=(4x2﹣y2+x2+2xy+y2﹣4x2+2xy)×(﹣![]() )
)
=(x2+4xy)×(﹣![]() )
)
=﹣2x﹣8y,
∵![]() +(y+4)2=0,
+(y+4)2=0,
∴x﹣5=0,y+4=0,
解得,x=5,y=﹣4,
∴当x=5,y=﹣4时,原式=﹣2×5﹣8×(﹣4)=﹣10+32=22.


科目:初中数学 来源: 题型:
【题目】如图所示,长方形纸片ABCD的长AD=9cm,宽AB=3cm,将其折叠,使点D与点B重合.
求:(1)折叠后DE的长;(2)以折痕EF为边的正方形面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了开展“阳光体育运动”,计划购买篮球、足球共60个,已知每个篮球的价格为70元,每个足球的价格为80元.
(1)若购买这两类球的总金额为4600元,求篮球、足球各买了多少个?
(2)若购买篮球的总金额不超过购买足球的总金额,求最多可购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在ABCD中,BF平分∠ABC交AD于点F,AE⊥BF于点O,交BC于点E,连接EF.
(1)求证:四边形ABEF是菱形:
(2)若菱形ABEF的周长为16,∠BEF=120°,求AE的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为筹备迎新生晚会,同学们设计了一个圆筒形灯罩,底色漆成白色,然后缠绕红色油纸.如图,已知圆筒高108cm,其圆筒底面周长为36cm,如果在表面缠绕油纸4圈,应裁剪油纸的最短为_____cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图.已知某开发区有一块四边形空地ABCD,现计划在该空地上种植草皮,经测量∠ADC=90°,AD=6m,CD=8m,BC=AB=13m,若每平方米草皮需200元,则在该空地上种植草皮共需多少钱?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
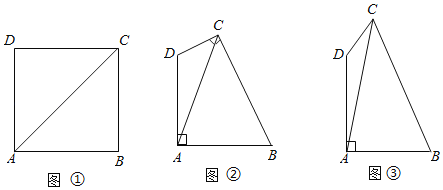
(1)如图①,在正方形ABCD中,对角线AC=8,则正方形ABCD的面积为 ;
问题探究
(2)如图②,在四边形ABCD中,AD=AB,∠DAB=∠DCB=90°,∠ADC+∠ABC=180°,若四边形ABCD的面积为8,求对角线AC的长;
问题解决
(3)如图③,四边形ABCD是张叔叔要准备开发的菜地示意图,其中边AD和AB是准备用砖来砌的砖墙,且满足AD=AB,∠DAB=90°,边DC和CB是准备用现有的长度分别为3米和7米的竹篱笆来围成的篱笆墙,即DC=3米,CB=7米.按照这样的想法,张叔叔围成的菜园里对角线AC的长是否存在最大值呢?若存在,求出这个最大值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),E是直线AB、CD内部一点,AB∥CD,连接EA、ED.
(1)探究:
①若∠A=30°,∠D=40°,则∠AED等于多少度?
②若∠A=20°,∠D=60°,则∠AED等于多少度?
③在图(1)中∠AED、∠EAB、∠EDC有什么数量关系,并证明你的结论.
(2)拓展:如图(2),射线FE与矩形ABCD的边AB交于点E,与边CD交于点F,①②③④分别是被射线FE隔开的四个区域(不含边界,其中③④位于直线AB的上方),P是位于以上四个区域上点,猜想:∠PEB、∠PFC、∠EPF之间的关系.(不要求证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
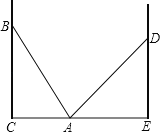
【题目】如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧的墙上时,梯子的顶端在B点,当它靠在另一侧的墙上时,梯子的顶端在D点,已知∠BAC=60°,点B到地面的垂直距离BC=5![]() 米,DE=6米.
米,DE=6米.
(1)求梯子的长度;
(2)求两面墙之间的距离CE.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com