
【题目】如图所示,D为△ABC的边AB的延长线上一点,过D作DF⊥AC,垂足为F,交BC于E,且BD=BE,求证:△ABC是等腰三角形.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
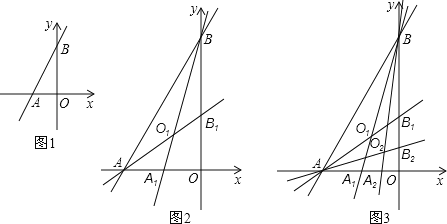
【题目】如图1,一次函数y=2x+4与x轴,y轴分别相交于A,B两点,一次函数图象与坐标轴围成的△ABO,我们称它为此一次函数的坐标三角形.把坐标三角形面积分成相等的二部分的直线叫做坐标三角形的等积线.
(1)求此一次函数的坐标三角形周长以及过点A的等积线的函数表达式;
(2)如图2,我们把第一个坐标三角形△ABO记为第一代坐标三角形.第一代坐标三角形的等积线BA1,AB1记为第一对等积线,它们交于点O1,四边形A1OB1O1称为第一个坐标四边形.求点O1的坐标和坐标四边形A1OB1O1面积;
(3)如图3.第一对等积线与坐标轴构成了第二代坐标三角形△BA1O.△AOB1分别过点A,B作一条平分△BA1O,△AOB1面积的第二对等积线BA2,AB2,相交于点O2,如此进行下去.…,请直接写出On的坐标和第n个坐标四边形面积(用n表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC沿直线l向右移了3厘米,得△FDE,且BC=6厘米,∠B=40°.
(1)求BE;
(2)求∠FDB的度数;
(3)找出图中相等的线段(不另添加线段);
(4)找出图中互相平行的线段(不另添加线段).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出定义:设一条直线与一条抛物线只有一个公共点,且这条直线与这条抛物线的对称轴不平行,就称直线与抛物线相切,这条直线是抛物线的切线.有下列命题: ①直线y=0是抛物线y= ![]() x2的切线;
x2的切线;
②直线x=﹣2与抛物线y= ![]() x2 相切于点(﹣2,1);
x2 相切于点(﹣2,1);
③若直线y=x+b与抛物线y= ![]() x2相切,则相切于点(2,1);
x2相切,则相切于点(2,1);
④若直线y=kx﹣2与抛物线y= ![]() x2相切,则实数k=
x2相切,则实数k= ![]() .
.
其中正确命题的是( )
A.①②④
B.①③
C.②③
D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD中,AB=4cm,BC=3cm,点E是CD的中点,动点P从A点出发,以每秒1cm的速度沿A→B→C→E 运动,最终到达点E.若点P运动的时间为x秒,那么当x= _________时,△APE的面积等于![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,OE⊥AB,OF⊥AC且OE=OF.
(1)如图,当点O在BC边中点时,试说明AB=AC;

(2)如图,当点O在△ABC内部时,且OB=OC,试说明AB与AC的关系;

(3)当点O在△ABC外部时,且OB=OC,试判断AB与AC的关系.(画出图形,写出结果即可,无须说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】比较下面每小题中两个算式结果的大小(在横线上填“>”、“<”或“=”).
⑴32+42 2×3×4;⑵22+22 2×2×2;⑶12+![]() 2×1×
2×1×![]() ;
;
⑷(-2) 2+52 2×(-2)×5;⑸![]()
![]()
通过观察上面的算式,请你用字母来表示上面算式中反映的一般规律.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作菱形ADEF(A、D、E、F按逆时针排列),使∠DAF=60°,连接CF.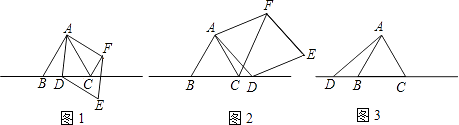
(1)如图1,当点D在边BC上时,求证:①BD=CF;②AC=CF+CD;
(2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CF+CD是否成立?若不成立,请写出AC、CF、CD之间存在的数量关系,并说明理由;
(3)如图3,当点D在边CB的延长线上且其他条件不变时,补全图形,并直接写出AC、CF、CD之间存在的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com