
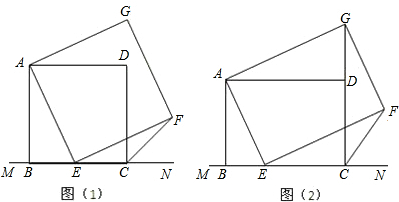
���� ��1�����������Ρ����ε������Լ�ͬ�ǵ������ȵõ���BAE=��DAG������ȫ�������ε��ж�����֤����BAE�ա�DAG��
��2����FH��MN��H��֤����EHF�ա�ABE���õ�FH=BE�����ݵ���ֱ�������ε����������FCN�Ķ�����
��3����FP��MN��P��֤����EFP�ա�AGD���õ�EP=AD=BC=b��֤����EFP�ס�AEB���������������ε����ʺ����еĸ����ɣ�
���  ��1��֤�������ı���ABCD�������Σ��ı���AEFG�Ǿ��Σ�
��1��֤�������ı���ABCD�������Σ��ı���AEFG�Ǿ��Σ�
��AB=AD����BAD=��EAG=��ABE=��ADG=90�㣬
���BAE+��EAD=��DAG+��EAD��
���BAE=��DAG��
�ڡ�ADG�͡�ABE�У�
$\left\{\begin{array}{l}{��BAE=��DAG}\\{AB=AD}\\{��ABE=��ADG}\end{array}\right.$
���BAE�ա�DAG��AAS����
��2����FCN=45�㣮
�������£���FH��MN��H��
�ߡ�AEF=��ABE=90�㣬
���BAE+��AEB=90�㣬��FEH+��AEB=90�㣬
���FEH=��BAE��
�ߡ�EBA=��FHE=90�㣬��BAE=��FEH��
��Rt��BAE��Rt��DAG��
��AE=AG=EF��
�ڡ�EHF�͡�ABE�У�
$\left\{\begin{array}{l}{��BAE=��HEF}\\{ABE=��EHF}\\{AE=EF}\end{array}\right.$��
���EHF�ա�ABE��AAS����
��FH=BE��EH=AB=BC��
��CH=BE=FH��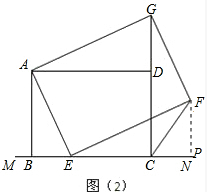
�ߡ�FHC=90�㣬
���FCH=45�㣻
��3������E��B��C�˶�ʱ����FCN�Ĵ�С�ܱ��ֲ��䣮
�������£���ͼ��2����FP��MN��P��
����֪�ɵá�EAG=��BAD=��AEF=90�㣬
��ϣ�1���á�FEH=��BAE=��DAG��
�֡�G������CD�ϣ����GDA=��EHF=��EBA=90�㣬
�ڡ�EFH�͡�AGD�У�
$\left\{\begin{array}{l}{��GDA=��FPE}\\{��DAG=��FEP}\\{AG=EF}\end{array}\right.$��
���EFP�ա�AGD��AAS����
��EP=AD=BC=b��CP=BE��
�ߡ�BAE=��FEP����ABE=��FPE��
���EFP�ס�AEB��
��$\frac{EP}{AB}=\frac{FP}{BE}=\frac{EP}{CP}$��
����Rt��FEH��tan��FCN=$\frac{FP}{CP}=\frac{EP}{AB}=\frac{b}{a}$��
�൱��E������CN�˶�ʱ��tan��FCN=$\frac{b}{a}$��
���� ���⿼����������κ;��ε����ʡ����������ε��ж������ʡ�ȫ�������ε��ж������ʣ��������������ε��ж����������ʶ�����ȫ�������ε��ж����������ʶ����ǽ���Ĺؼ���


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
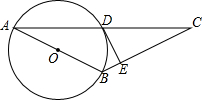 ��ͼ��ABΪ��O��ֱ������O��AC���е�D��DEΪ��O�����ߣ�
��ͼ��ABΪ��O��ֱ������O��AC���е�D��DEΪ��O�����ߣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
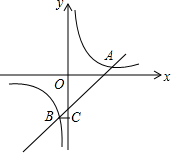 ��ͼ����ƽ��ֱ������ϵ�У�˫����y=$\frac{m}{x}$��ֱ��y=kx+b����A��B���㣬A��5��1����BC��y����C����OC=5BC��
��ͼ����ƽ��ֱ������ϵ�У�˫����y=$\frac{m}{x}$��ֱ��y=kx+b����A��B���㣬A��5��1����BC��y����C����OC=5BC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��1�����㣨-1��2013+2sin60��+����-3.14��0+|-$\sqrt{3}$|��
��1�����㣨-1��2013+2sin60��+����-3.14��0+|-$\sqrt{3}$|���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABC���ܳ�Ϊ24��AC�Ĵ�ֱƽ���߽�BC�ڵ�D������ΪE����AE=4�����ADB���ܳ���16��
��ͼ����ABC���ܳ�Ϊ24��AC�Ĵ�ֱƽ���߽�BC�ڵ�D������ΪE����AE=4�����ADB���ܳ���16���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
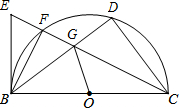 ��ͼ��ֱ��Ϊ10�İ�ԲO��tan��DBC=$\frac{3}{4}$����BCD��ƽ���߽���O��F��EΪCF�ӳ�����һ�㣬�ҡ�EBF=��GBF��
��ͼ��ֱ��Ϊ10�İ�ԲO��tan��DBC=$\frac{3}{4}$����BCD��ƽ���߽���O��F��EΪCF�ӳ�����һ�㣬�ҡ�EBF=��GBF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
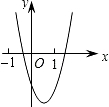 ���κ���y=ax2+bx+c��ͼ����ͼ��ʾ����һ�κ���y=ax-c�뷴��������y=$\frac{a+b+c}{x}$��ͬһ����ϵ�ڵ�ͼ�����Ϊ��������
���κ���y=ax2+bx+c��ͼ����ͼ��ʾ����һ�κ���y=ax-c�뷴��������y=$\frac{a+b+c}{x}$��ͬһ����ϵ�ڵ�ͼ�����Ϊ��������| A�� | 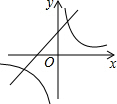 | B�� | 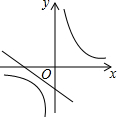 | C�� | 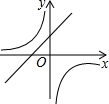 | D�� | 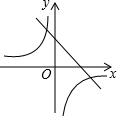 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com