练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    5．在-2.5，$\frac{1}{3}$，0，2这四个数中，最小的数是（　　）
    A．-2.5B．$\frac{1}{3}$C．0D．2

    分析 有理数大小比较的法则：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小，据此判断即可．

    解答 解：根据有理数比较大小的方法，可得
    -2.5＜0＜$\frac{1}{3}$＜2，
    ∴在-2.5，$\frac{1}{3}$，0，2这四个数中，最小的数是-2.5．
    故选：A．

    点评 此题主要考查了有理数大小比较的方法，要熟练掌握，解答此题的关键是要明确：①正数都大于0；②负数都小于0；③正数大于一切负数；④两个负数，绝对值大的其值反而小．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    15．如图，把一块直角三角板的直角顶点放在直尺的一边上，若∠1=48°，则∠2的度数为（　　）
    A．48°B．42°C．40°D．45°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

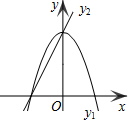    16．如图，已知抛物线y1=-2x2+2，直线y2=2x+2，当x任取一值时，x对应的函数值分别为y1、y2．若y1≠y2，取y1、y2中的较小值记为M；若y1=y2，记M=y1=y2．例如：当x=1时，y1=0，y2=4，y1＜y2，此时M=0．下列判断：
    ①当x＞0时，y1＞y2；②当x＜0时，x值越大，M值越小； ③使得M大于2的x值不存在；④使得M=1的x值是-$\frac{1}{2}$或$\frac{\sqrt{2}}{2}$．
    其中正确的个数是（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

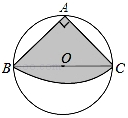    13．如图，从一块圆形纸片上剪出一个圆心角为90°的扇形ABC，使点A、B、C在圆周上，
    将剪下的扇形作为一个圆锥侧面，如果圆锥的高为3$\sqrt{30}$cm，则这块圆形纸片的直径为（　　）
    A．12cmB．20cmC．24cmD．28cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

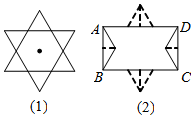    20．小东同学对图形世界充满兴趣，他先把一个面积为$\frac{27}{4}\sqrt{3}$cm2的正三角形绕着它的中心旋转60°，旋转前后的两个正三角形构成如图（1）的一个六角星；然后将该六角星按图（2）分割后拼成矩形ABCD．请你思考小东的问
    题：若将该矩形围成圆柱，则圆柱的高为（　　）
    A．2$\sqrt{3}$cmB．3$\sqrt{3}$cmC．2$\sqrt{3}$cm 或6 cmD．3cm或3$\sqrt{3}$cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．对于实数a、b，定义一种新运算“?”为：a?b=$\frac{1}{a-{b}^{2}}$，这里等式右边是实数运算．例如：1?3=$\frac{1}{1-{3}^{2}}$=-$\frac{1}{8}$．则方程x?（-2）=$\frac{2}{x-4}$-1的解是x=5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．在实数-2，$\sqrt{2}$，0，-1中，最小的数是（　　）
    A．-2B．$\sqrt{2}$C．0D．-1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

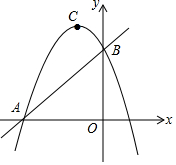    14．如图，直线y=x+n与x轴交于点A，与y轴交于点B（点A与点B不重合），抛物线y=-$\frac{1}{2}$x2-2x+c经过点A、B，抛物线的顶点为C．
    （1）∠BAO=45°；
    （2）求tan∠CAB的值；
    （3）在抛物线上是否存在点P，能够使∠PCA=∠BAC？如果存在，请求出点P的坐标；如果不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．在四边形ABCD中，对角线AC⊥BD且AC=4、BD=6．E、F分别是边AB、CD的中点，则EF=$\sqrt{13}$．

    查看答案和解析>>

    同步练习册答案