
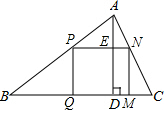
 如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成长方形零件PQMN,使长方形PQMN的边QM在BC上,其余两个顶点P,N分别在AB,AC上,求这个长方形零件PQMN面积S的最大值.
如图,△ABC是一块锐角三角形余料,边BC=120mm,高AD=80mm,要把它加工成长方形零件PQMN,使长方形PQMN的边QM在BC上,其余两个顶点P,N分别在AB,AC上,求这个长方形零件PQMN面积S的最大值. 分析 设长方形零件PQMN的边PN=a,PQ=x,则AE=80-x,利用△APN∽△ABC得相似比,用相似比可得出用含x的式子表示a,故S=x•a,从而得出二次函数解析式,根据解析式及自变量取值范围求S的最大值.
解答 解:设长方形零件PQMN的边PN=a,PQ=x,则AE=80-x.
∵PN∥BC,
∴△APN∽△ABC.
∴$\frac{PN}{BC}$=$\frac{AE}{AD}$.
因此,$\frac{a}{120}$=$\frac{80-x}{80}$.
解得a=120-$\frac{3}{2}$x.
所以长方形PQMN的面积S=xa=x(120-$\frac{3}{2}$x)=-$\frac{3}{2}$x2+120x.(3分)
当x=-$\frac{120}{2×(-\frac{3}{2})}$=40时,a=60.(4分)
S最大值=40×60=2400(mm2).
所以这个长方形零件PQMN面积S的最大值是2400mm2.
点评 本题用二次函数的方法解决面积问题,是函数性质的实际运用,需要从计算矩形面积着手,求矩形的长、宽.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 品名 | 番茄 | 豆角 |
| 批发价/(元/千克) | 2.4 | 3.2 |
| 零售价/(元/千克) | 3.6 | 5.0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com