
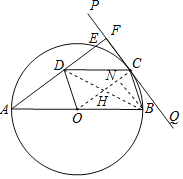
【题目】如图,AB是⊙O的直径,直线PQ与⊙O相切于点C,以OB,BC为边作OBCD,连接AD并延长交⊙O于点E,交直线PQ于点F.
(1)求证:AF⊥CF;
(2)连接OC,BD交于点H,若tan∠OCB=3,⊙O的半径是5,求BD的长.

【答案】(1)见解析;(2)![]()
【解析】
(1)连接OC,如图,根据平行四边形的性质得到DC∥OB,DC=OB,推出四边形OCDA是平行四边形,得到AF∥OC,根据切线的性质得到∠OCQ=90°,于是得到结论;
(2)过点B作BN⊥OC于点N,如图,根据平行四边形的性质得到BD=2BH,![]() ,
,![]() ,设CN=x,BN=3x,求得ON=5﹣x,根据勾股定理即可得到结论.
,设CN=x,BN=3x,求得ON=5﹣x,根据勾股定理即可得到结论.
(1)证明:连接OC,如图,
∵四边形OBCD是平行四边形,
∴DC∥OB,DC=OB,
∵AO=OB,
∴DC∥AO,DC=AO,
∴四边形OCDA是平行四边形,
∴AF∥OC,
∵直线PQ与⊙O相切于点C,OC是半径,
∴∠OCQ=90°,
∴∠AFC=∠OCQ=90°,
即AF⊥CF;
(2)过点B作BN⊥OC于点N,如图,
∵四边形OBCD是平行四边形,
∴BD=2BH,![]() .
.
在Rt△BNC中,![]() ,
,
设CN=x,BN=3x,
∴ON=5﹣x.
在Rt△ONB中,(5﹣x)2+(3x)2=52,
解得x1=0(舍),x2=1.
∴BN=3x=3,![]() .
.
在Rt△HNB中,由勾股定理可得![]() .
.
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】党的十八大以来,全国各地认真贯彻精准扶贫方略,扶贫工作力度、深度和精准度都达到了新的水平,为2020年全面建成小康社会的战略目标打下了坚实基础.以下是根据近几年中国农村贫困人口数量(单位:万人)及分布情况绘制的统计图表的一部分.
年份 人数 地区 | 2017 | 2018 | 2019 |
东部 | 300 | 147 | 47 |
中部 | 1112 | 181 | |
西部 | 1634 | 916 | 323 |
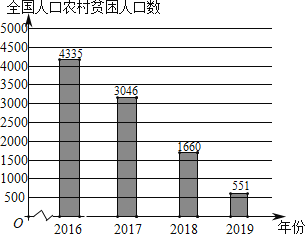
(以上数据来源于国家统计局)
根据统计图表提供的信息,下面推断不正确的是( )
A.2018年中部地区农村贫困人口为597万人
B.2017﹣2019年,农村贫困人口数量都是东部最少
C.2016﹣2019年,农村贫困人口减少数量逐年增多
D.2017﹣2019年,虽然西部农村贫困人口减少数量最多,但是相对于东、中部地区,它的降低率最低
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国务院发布的《全民科学素质行动计划纲要实施方案(2016-2020年)》指出:公民科学素质是实施创新驱动发展战略的基础,是国家综合国力的体现.《方案》明确提出,2020年要将我国公民科学素质的数值提升到10%以上.为了解我国公民科学素质水平及发展状况,中国科协等单位已多次组织了全国范围的调查,以下是根据调查结果整理得到的部分信息.注:科学素质的数值是指具备一定科学素质的公民人数占公民总数的百分比.
![]() .2015和2018年我国各直辖市公民科学素质发展状况统计图如下:
.2015和2018年我国各直辖市公民科学素质发展状况统计图如下:
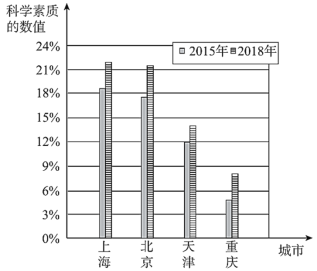
b.2015年和2018年我国公民科学素质发展状况按性别分类统计如下:
2015年 | 2018年 | |
男 |
|
|
女 |
|
|
c.2001年以来我国公民科学素质水平发展统计图如下:
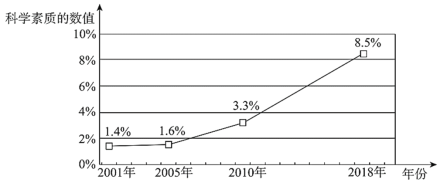
根据以上信息,回答下列问题:
(1)在我国四个直辖市中,从2015年到2018年,公民科学素质水平增幅最大的城市是________,公民科学素质水平增速最快的城市是_________.注:科学素质水平增幅=2018年科学素质的数值一2015年科学素质的数值;科学素质水平增速=(2018年科学素质的数值一2015年科学素质的数值)÷2015年科学素质的数值.
(2)已知在2015年的调查样本中,男女公民的比例约为1:1,则2015年我国公民的科学素质水平为______%(结果保留一位小数);由计算可知.在2018年的调查样本中.男性公民人数_____女性公民人数(填“多于”、“等于”或“少于”).
(3)根据截至2018年的调查数据推断,你认为“2020年我国公民科学素质提升到10%以上”的目标能够实现吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD为矩形,曲线L经过点D.点Q是四边形ABCD内一定点,点P是线段AB上一动点,作PM⊥AB交曲线L于点M,连接QM.
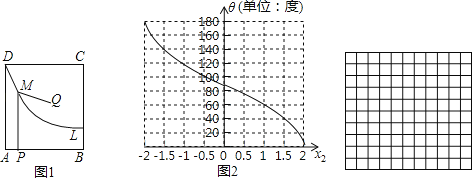
小东同学发现:在点P由A运动到B的过程中,对于x1=AP的每一个确定的值,θ=∠QMP都有唯一确定的值与其对应,x1与θ的对应关系如表所示:
x1=AP | 0 | 1 | 2 | 3 | 4 | 5 |
θ=∠QMP | α | 85° | 130° | 180° | 145° | 130° |
小芸同学在读书时,发现了另外一个函数:对于自变量x2在﹣2≤x2≤2范围内的每一个值,都有唯一确定的角度θ与之对应,x2与θ的对应关系如图2所示:
根据以上材料,回答问题:
(1)表格中α的值为 .
(2)如果令表格中x1所对应的θ的值与图2中x2所对应的θ的值相等,可以在两个变量x1与x2之间建立函数关系.
①在这个函数关系中,自变量是 ,因变量是 ;(分别填入x1和x2)
②请在网格中建立平面直角坐标系,并画出这个函数的图象;
③根据画出的函数图象,当AP=3.5时,x2的值约为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了做到合理用药,使药物在人体内发挥疗效作用,该药物的血药浓度应介于最低有效浓度与最低中毒浓度之间.某成人患者在单次口服1单位某药后,体内血药浓度及相关信息如图:
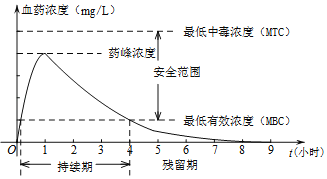
根据图中提供的信息,下列关于成人患者使用该药物的说法中:
①首次服用该药物1单位约10分钟后,药物发挥疗效作用;
②每间隔4小时服用该药物1单位,可以使药物持续发挥治疗作用;
③每次服用该药物1单位,两次服药间隔小于2.5小时,不会发生药物中毒.
所有正确的说法是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
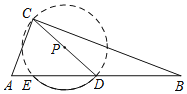
【题目】在△ABC中,以AB边上的中线CD为直径作圆,如果与边AB有交点E(不与点D重合),那么称![]() 为△ABC的C﹣中线弧.例如,如图中
为△ABC的C﹣中线弧.例如,如图中![]() 是△ABC的C﹣中线弧.在平面直角坐标系xOy中,已知△ABC存在C﹣中线弧,其中点A与坐标原点O重合,点B的坐标为(2t,0)(t>0).
是△ABC的C﹣中线弧.在平面直角坐标系xOy中,已知△ABC存在C﹣中线弧,其中点A与坐标原点O重合,点B的坐标为(2t,0)(t>0).
(1)当t=2时,
①在点C1(﹣3,2),C2(0,2![]() ),C3(2,4),C4(4,2)中,满足条件的点C是 ;
),C3(2,4),C4(4,2)中,满足条件的点C是 ;
②若在直线y=kx(k>0)上存在点P是△ABC的C﹣中线弧![]() 所在圆的圆心,其中CD=4,求k的取值范围;
所在圆的圆心,其中CD=4,求k的取值范围;
(2)若△ABC的C﹣中线弧![]() 所在圆的圆心为定点P(2,2),直接写出t的取值范围.
所在圆的圆心为定点P(2,2),直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
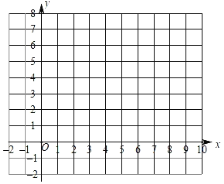
【题目】在平面直角坐标系xOy中,直线x=5与直线y=3,x轴分别交于点A,B,直线y=kx+b(k≠0)经过点A且与x轴交于点C(9,0).
(1)求直线y=kx+b的表达式;
(2)横、纵坐标都是整数的点叫做整点.记线段AB,BC,CA围成的区域(不含边界)为W.
①结合函数图象,直接写出区域W内的整点个数;
②将直线y=kx+b向下平移n个单位,当平移后的直线与区域W没有公共点时,请结合图象直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,AB,CD,EF,GH是正方形OPQR边上的线段,点M在其中某条线段上,若射线OM与x轴正半轴的夹角为α,且sinα>cosα,则点M所在的线段可以是( )
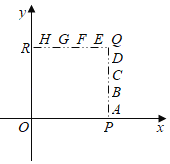
A.AB和CDB.AB和EFC.CD和GHD.EF和GH
查看答案和解析>>
科目:初中数学 来源: 题型:
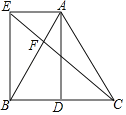
【题目】如图,在△ABC中,AB=AC,D为BC中点,AE∥BD,且AE=BD.
(1)求证:四边形AEBD是矩形;
(2)连接CE交AB于点F,若∠ABE=30°,AE=2,求EF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com