

分析 (1)先根据共支付给旅行社旅游费用15750元,确定旅游的人数的范围;
(2)根据每人的旅游费用×人数=总费用,设该单位这次共有x名员工去旅游.即可由对话框,超过20人的人数为(x-20)人,每人降低10元,共降低了10(x-20)元.实际每人收了[600-10(x-20)]元,列出方程求解.
解答 解:(1)设该单位这次共有x名员工去旅游.
因为600×20=12000<15750,所以员工人数一定超过20人.
(2)设该单位这次共有x名员工去旅游,根据题意列方程得:
[600-10(x-20)]x=15750.
整理得x2-80x+1575=0,
即(x-45)(x-35)=0,
解得x1=45,x2=35.
当x1=45时,600-10(x-20)=350<420,故舍去x1;
当x2=35时,600-10(x-20)=450>420,符合题意.
答:该单位这次共有35名员工去旅游.
点评 此题考查了一元二次方程的应用,此类题目贴近生活,有利于培养学生应用数学解决生活中实际问题的能力.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.本题应注意的地方有两点:1、确定人数的范围;2、用人均旅游费用不低于420元来判断,得到满足题意的x的值.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
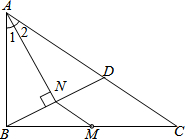 如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=6,BC=8,MN=2.
如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=6,BC=8,MN=2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
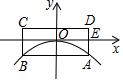 如图在平面直角坐标系中,矩形ABCD的顶点A、B在抛物线y=ax2上,且AB平行于x轴,AD的中点E在x轴上,AB=2AD.若矩形ABCD周长为18,则a的值为-$\frac{1}{6}$.
如图在平面直角坐标系中,矩形ABCD的顶点A、B在抛物线y=ax2上,且AB平行于x轴,AD的中点E在x轴上,AB=2AD.若矩形ABCD周长为18,则a的值为-$\frac{1}{6}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com