
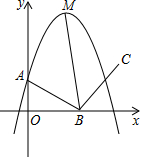
 如图,抛物线y=-2x2+4x+1交y轴点A,顶点是M,点B是x轴上的一个动点,连结AB,BM,将线段AB绕点B顺时针旋转90°到BC的位置,当BM平分∠ABC时,点B的坐标是(1,0)或(2,0).
如图,抛物线y=-2x2+4x+1交y轴点A,顶点是M,点B是x轴上的一个动点,连结AB,BM,将线段AB绕点B顺时针旋转90°到BC的位置,当BM平分∠ABC时,点B的坐标是(1,0)或(2,0). 分析 根据抛物线的解析式求得A、M的坐标,设B(a,0),作CD⊥x轴于D,证得△AOB≌△BDC,求得BD=OA=1,CD=OB=a,得出C(1+a,a),然后证得△AMB≌△CMB,求得AM=CM,进而根据勾股定理得出关于a的方程,解方程即可求得.
解答 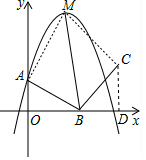 解:∵抛物线y=-2x2+4x+1=-2(x-1)+3交y轴点A,顶点是M,
解:∵抛物线y=-2x2+4x+1=-2(x-1)+3交y轴点A,顶点是M,
∴A(0,1),M(1,3),
设B(a,0),
作CD⊥x轴于D,
∵∠ABC=90°,
∴∠ABO+∠CBD=90°,
∵∠ABO+∠OAB=90°,
∴∠OAB=∠CBD,
∵∠AOB=∠BDC=90°,
在△AOB和△BDC中
$\left\{\begin{array}{l}{∠OAB=∠CBD}\\{∠AOB=∠BDC}\\{AB=BC}\end{array}\right.$
∴△AOB≌△BDC,
∴BD=OA=1,CD=OB=a,
∴C(1+a,a),
在△AMB和△CMB中
$\left\{\begin{array}{l}{AB=BC}\\{∠ABM=∠CBM}\\{BM=BM}\end{array}\right.$
∴△AMB≌△CMB,
∴AM=CM,
∴(1+a-1)2+(a-3)2=(0-1)2+(1-3)2,
解得a1=2,a2=1,
∴B(2,0)或(1,0).
故答案为(2,0)或(1,0).
点评 本题考查了二次函数的图象于几何变换,三角形全等的判定和性质,勾股定理的应用等,作出辅助线构建全等三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
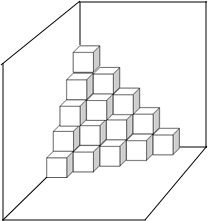 如图,是按规律摆放在墙角的一些小正方体,从上往下分别记为第一层,第二层,第三层…第n层…
如图,是按规律摆放在墙角的一些小正方体,从上往下分别记为第一层,第二层,第三层…第n层…查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
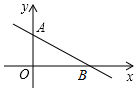 平面直角坐标系中,直线y=-$\frac{1}{2}$x+2和x、y轴交于A、B两点,在第二象限内找一点P,使△PAO和△AOB相似的三角形个数为( )
平面直角坐标系中,直线y=-$\frac{1}{2}$x+2和x、y轴交于A、B两点,在第二象限内找一点P,使△PAO和△AOB相似的三角形个数为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
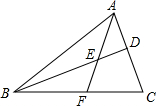 如图,在△ABC中,点D在AC上,点E在BD上,且$\frac{AD}{DC}$=$\frac{2}{3}$,$\frac{BE}{ED}$=$\frac{3}{2}$,AE的延长线交BC于点F,求BF:FC.
如图,在△ABC中,点D在AC上,点E在BD上,且$\frac{AD}{DC}$=$\frac{2}{3}$,$\frac{BE}{ED}$=$\frac{3}{2}$,AE的延长线交BC于点F,求BF:FC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com