
分析 (1)根据十字相乘法分解因式进行分解即可.
(2)先去括号,然后由完全平方公式进行因式分解.
(3)根据观察看出①中x的系数为1,故用代入法消元较好,把①变形成含y的代数式表示x,再把其代入②便可消去x,解出y的值,再把y的值代入变形后的式子,即可得到x的值.
解答 解:(1)x2-5x+6=(x-2)(x-3).
(2)(x-3)(x+1)+4=x2-2x-3+4=(x-1)2.
(3)$\left\{\begin{array}{l}{x-2y=1①}\\{3x-5y=8②}\end{array}\right.$,
由①得,x=2y+1,③
把③代入②,得
3(2y+1)-5y=8,
解得y=5.
则x=2×5+1=11.
所以原方程组的解为:$\left\{\begin{array}{l}{x=11}\\{y=5}\end{array}\right.$.
点评 本题考查了因式分解和二元一次方程组的解法.运用十字相乘法分解因式时,要注意观察,尝试,并体会它实质是二项式乘法的逆过程.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:填空题
 最近重庆八中学生宿舍在增修安全通道,一辆拉砖的货车从仓库匀速驶往学校,到达后用了1小时卸货,随即匀速返回.已知货车返回的速度是它从仓库驶往学饺的速度的2倍,货车离仓库的距离y(千米)关于时间x的函数图象如图所示.则a=4.5(小时).
最近重庆八中学生宿舍在增修安全通道,一辆拉砖的货车从仓库匀速驶往学校,到达后用了1小时卸货,随即匀速返回.已知货车返回的速度是它从仓库驶往学饺的速度的2倍,货车离仓库的距离y(千米)关于时间x的函数图象如图所示.则a=4.5(小时).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
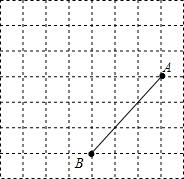 请在网格中建立平面直角坐标系,使得A点的坐标为(4,2).
请在网格中建立平面直角坐标系,使得A点的坐标为(4,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A种水果/箱 | B种水果/箱 | |
| 甲店 | 11元 | 17元 |
| 乙店 | 9元 | 13元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com