
已知:如图,正方形ABCD中, CM=CD,MN⊥AC,连结CN,则∠DCN=_____=____∠B,∠MND=_______=_______∠B.

22.5,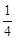 ,67.5°,
,67.5°,
【解析】
试题分析:在Rt△MNC和Rt△DNC中,MC=DC,NC=NC,根据勾股定理即可得MN=DN,即可证明Rt△MNC≌Rt△DNC,故∠DCN= ∠DCA,即可计算∠MNC.
∠DCA,即可计算∠MNC.
在Rt△MNC和Rt△DNC中,CM=CD,NC=NC
∴根据勾股定理可以求得MN=DN,
∴Rt△MNC≌Rt△DNC,
∴∠DCN=∠MCN,
∵正方形对角线AC即角平分线,
∴∠DCN= ∠DCA=22.5°,
∠DCA=22.5°,
∵∠MNC+∠MCN=90°,
∴∠MCN=90°-22.5°=67.5°,
∵∠B=90°,
∴∠DCN=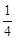 ∠B,∠MNC=
∠B,∠MNC= ∠B.
∠B.
考点:本题考查了正方形的性质,全等三角形的判定和性质
点评:解答本题的关键是熟练掌握正方形各边长相等、各内角均为直角,全等三角形对应角相等.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
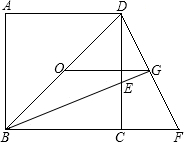 ,连接DF,交BE的延长线于点G,连接OG.
,连接DF,交BE的延长线于点G,连接OG.| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 32 |
| x |
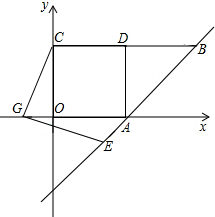
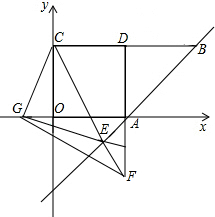
| OG+GF |
| DF |
查看答案和解析>>
科目:初中数学 来源: 题型:



查看答案和解析>>
科目:初中数学 来源: 题型:
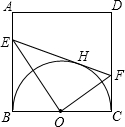 于E,交CD于F.
于E,交CD于F.| 13 | 48 |
查看答案和解析>>
科目:初中数学 来源: 题型:
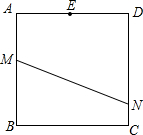 已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.
已知:如图,正方形纸片ABCD的边长是4,点M、N分别在两边AB和CD上(其中点N不与点C重合),沿直线MN折叠该纸片,点B恰好落在AD边上点E处.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com