
【题目】结合数轴与绝对值的知识回答下列问题:
![]()
(1)数轴上表示![]() 和
和![]() 的两点之间的距离是__________;表示
的两点之间的距离是__________;表示![]() 和
和![]() 两点之间的距离是__________;
两点之间的距离是__________;
(2)如果![]() ,那么
,那么![]() __________;
__________;
(3)若![]() ,
,![]() ,且数
,且数![]() 、
、![]() 在数轴上表示的点分别是点
在数轴上表示的点分别是点![]() 、点
、点![]() ,则
,则![]() 、
、![]() 两点间的最大距离是_____,最小距离是______;
两点间的最大距离是_____,最小距离是______;
(4)求代数式![]() 的最小值,并写出此时
的最小值,并写出此时![]() 可取哪些整数值?
可取哪些整数值?
(5)求代数式![]() 的最小值.
的最小值.
(6)若![]() 表示一个有理数,则代数式
表示一个有理数,则代数式![]() 有最大值吗?若有,请求出最大值;若没有,请说明理由.
有最大值吗?若有,请求出最大值;若没有,请说明理由.
【答案】(1)3,5;(2)1或-3;(3)12,2;(4)最小值为2,x的整数值为: -1,0,1;(5)7;(6)4.
【解析】
(1)根据数轴点坐标意义,求出两个数的差的绝对值即可;
(2)根据绝对值的意义解方程即可;
(3)根据绝对值分别求出a,b的值,再分别讨论,即可求出最大值和最小值.
(4)求![]() 的最小值,即找一点到坐标为-1和1的点距离和最小.由线段的性质,两点之间,线段最短,可知当-1≤x≤1时,
的最小值,即找一点到坐标为-1和1的点距离和最小.由线段的性质,两点之间,线段最短,可知当-1≤x≤1时,![]() 有最小值,从而可求得最小值,利用数轴即可找到此时x可取的整数值.
有最小值,从而可求得最小值,利用数轴即可找到此时x可取的整数值.
(5)可以用数形结合来解题:![]() 为数轴上的一点,
为数轴上的一点,![]() 表示:点
表示:点![]() 到数轴上的3个点-2、3、5的距离之和,进而分析得出最小值.
到数轴上的3个点-2、3、5的距离之和,进而分析得出最小值.
(6)![]() 可化为
可化为![]() ,当
,当![]() 取最小值时,
取最小值时,![]() 取最大值,结合(4)可知当3≤x≤5时,
取最大值,结合(4)可知当3≤x≤5时,![]() 式子取最大值.
式子取最大值.
解:(1)∵![]() ,
,![]() ,
,
∴数轴上表示![]() 和
和![]() 的两点之间的距离是3;表示
的两点之间的距离是3;表示![]() 和
和![]() 两点之间的距离是5;
两点之间的距离是5;
故答案为:3;5.
(2)∵![]() ,
,
∴![]() ,
,
∴解得x=1或-3,
故答案为:1或-3.
(3)∵|a-3|=4,|b+2|=3,
∴a=7或-1,b=1或b=-5,
当a=7,b=-5时,则A、B两点间的最大距离是12,
当a=1,b=-1时,则A、B两点间的最小距离是2,
则A、B两点间的最大距离是12,最小距离是2;
故答案为12;2.
(4)根据题意可知,|x+1|+|x-1|有最小值即是x到1的距离与到1的距离之和最小,那么x应在1和3之间的线段上.
即当-1≤x≤1时,|x+1|+|x-1|有最小值.
∴|x+1|=x+1,|x-1|=1-x,
∴|x+3|+|x-4|=x+1+1-x=2;
由数轴可知,-1≤x≤1,x的整数值为: -1,0,1.
∴|x+1|+|x-1|的最小值为2,此时![]() 可取的整数值为: -1,0,1.
可取的整数值为: -1,0,1.
(5)∵![]() 表示:点
表示:点![]() 到数轴上的3个点-2、3、5的距离之和,即当x在中间点3时,距离之和最小.
到数轴上的3个点-2、3、5的距离之和,即当x在中间点3时,距离之和最小.
∴当x=3时,代数式![]() 有最小值,
有最小值,
最小值=![]() =7.
=7.
故代数式![]() 的最小值是7.
的最小值是7.
(6)∵![]() =
=![]() ,
,
∴当![]() 取最小值时,
取最小值时,![]() 取最大值,
取最大值,
∴由题可知,当3≤x≤5时,![]() 取最大值,
取最大值,
当3≤x≤5时,
![]() ,
,
=![]() ,
,
=8-2x+6+2x-10
=4,
故当3≤x≤5时,![]() 取最大值为4,
取最大值为4,


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,函数y=![]() (k>0,x>0)的图象与直线y=2x﹣2交于点Q(2,m).
(k>0,x>0)的图象与直线y=2x﹣2交于点Q(2,m).
(1)求m,k的值;
(2)已知点P(a,0)(a>0)是x轴上一动点,过点P作平行于y轴的直线,交直线y=2x﹣2于点M,交函数y=![]() 的图象于点N.
的图象于点N.
①当a=4时,求MN的长;
②若PM>PN,结合图象,直接写出a的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某天早晨,王老师从家出发步行前往学校,途中在路边一饭店吃早餐,如图所示是王老师从家到学校这一过程中的所走路程s(米)与时间t(分)之间的关系.
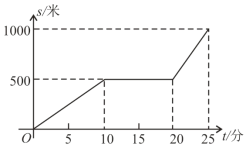
(1)学校离他家 米,从出发到学校,王老师共用了 分钟;王老师吃早餐用了 分钟?
(2)观察图形直接回答王老师吃早餐以前的速度快还是吃完早餐以后的速度快?
(3)求出王老师吃完早餐后的平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线AB:y=-x+b分别与x、y轴交于A(3,0)、B两点.

(1)如图,求点B的坐标;
(2)点D为线段OB上的动点(点D不与点O重合),以AD为边,在第一象限内作正方形ADEF.
①如图,设点D为(0,m),请用含m的代数式表示点F的坐标;
②如图,连结EB并延长交x轴于点G.当D点运动时,G点的位置是否发生变化?如果不变,请求出G点的坐标;如果变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有30箱苹果,以每箱20千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质质量的差 (单位:千克) |
|
|
| 1 | 2 |
箱数 | 2 | 6 | 10 | 8 | 4 |
(1)这30箱苹果中,最重的一箱比最轻的一箱重多少千克?
(2)与标准质量比较,这30箱苹果总计超过或不足多少千克?
(3)若苹果每千克售价6元,则出售这30箱苹果可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式的规律,解答下列问题:
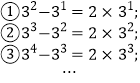
(1)按此规律,第④个等式为_________;第![]() 个等式为_______;(用含
个等式为_______;(用含![]() 的代数式表示,
的代数式表示,![]() 为正整数)
为正整数)
(2)按此规律,计算:
![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点C在AOB的一边OA上,过点C的直线DE//OB,CF平分ACD,CG CF于C .
(1)若O =40,求ECF的度数;
(2)求证:CG平分OCD;
(3)当O为多少度时,CD平分OCF,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某批发市场对外批发某品脾的玩具,其价格与件数关系如图所示,请你根据图中描述判断:下列说法中错误的是( )

A. 当件数不超过30件时,每件价格为60元
B. 当件数在30到60之间时,每件价格随件数增加而减少
C. 当件数为50件时,每件价格为55元
D. 当件数不少于60件时,每件价格都是45元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com