
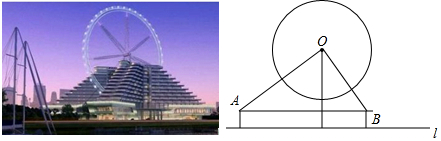
���� �ȸ�������ó���OAD=50�㣬��OBD=70�㼴�ɵó���AOD=40�㣬��BOD=20�㣬������뾶r��ʾ��OD=r+3�����������Ǻ�����ʾ��AD��BD����AB=12�������̼��ɣ�
��� �⣺��ͼ��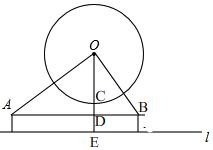 ��Ħ���ֵİ뾶Ϊr��
��Ħ���ֵİ뾶Ϊr��
��OC=r��
��Ħ���ֵĵײ������ĸ߶�Ϊ4�ף�
��CE=4��
�߲���ǵĸ߶�Ϊ1�ף�
��DE=1��
��CD=CE-DE=3��
��OD=OC+CD=r+3��
����A�����Ħ��������O������Ϊ50�㣬
���OAD=50�㣬
���AOD=90��-��OAD=40�㣬
����B�����Ħ��������O������Ϊ70�㣬
���OBD=70�㣬
���BOD=90��-��OBD=20�㣬
��Rt��ADO�У���AOD=40�㣬OD=r+3��
��tan��AOD=$\frac{AD}{OD}$��
��AD=OD•tan��AOD=��r+3��tan40���0.8��r+3����
��Rt��BDO�У���BOD=40�㣬OD=r+3��
��tan��BOD=$\frac{BD}{OD}$��
��BD=OD•tan��BOD=��r+3��tan20���0.4��r+3����
��AB��ľ���Ϊ12�ף�
��AB=12��
��AD+BD=12��
��0.8��r+3��+0.4��r+3��=12��
��r=7�ף�
��Ħ���ֵİ뾶Լ7�ף�
���� �����ǽ�ֱ�������ε�Ӧ��--���Ǹ��ǣ���Ҫ���������Ǹ��ǵ����壬ֱ�������ε����ʣ�������Ǻ������Ȿ��Ĺؼ����ð뾶��ʾ��AD��BD����һ�������⣮


 һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -2+a��-2+b | B�� | -$\frac{a}{2}$��-$\frac{b}{2}$ | C�� | -2a��-2b | D�� | a-3��b-3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{6}$ | B�� | 8 | C�� | $\frac{1}{8}$ | D�� | $\frac{3}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{2}{3}$ | B�� | -$\frac{3}{2}$ | C�� | -6 | D�� | $\frac{3}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | 2��4 | B�� | 1��4 | C�� | 3��4 | D�� | 3��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 9cm | B�� | 3cm | C�� | 3cm��9cm | D�� | 6cm��9cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y=��x+1��2-2 | B�� | y=-��x-1��2-2 | C�� | y=-��x-1��2+2 | D�� | y=��x-1��2-2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com