
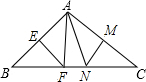
 如图,△ABC中,∠BAC=110°,EF,MN分别为AB,AC的垂直平分线,如果BC长为不等式3x-1<4x-5的最小整数解,那么△FAN的周长为5cm,∠FAN=40°.
如图,△ABC中,∠BAC=110°,EF,MN分别为AB,AC的垂直平分线,如果BC长为不等式3x-1<4x-5的最小整数解,那么△FAN的周长为5cm,∠FAN=40°. 分析 先求出BC的值,根据线段垂直平分线性质得出AF=BF,AN=CN,推出∠B=∠BAF,∠C=∠CAN,即可求出答案.
解答 解:∵不等式3x-1<4x-5得:x>4,
又∵BC长为不等式3x-1<4x-5的最小整数解,
∴BC=5,
∵EF,MN分别为AB,AC的垂直平分线,
∴BF=AF,AN=CN,
∴△FAN的周长为AF+FN+AN=NF+FN+CN=BC=5,
∠B=∠BAF,∠C=∠CAN,
∵△ABC中,∠BAC=110°,
∴∠B+∠C=180°-110°=70°,
∴∠FAN=∠BAC-(∠BAF+∠CAN)=∠BAC-(∠B+∠C)=110°-70°=40°,
故答案为:5,40°.
点评 本题考查了线段垂直平分线性质,三角形内角和定理,等腰三角形的性质的应用,能灵活运用线段垂直平分线性质进行推理是解此题的关键.


科目:初中数学 来源: 题型:填空题
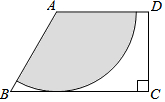 如图,梯形ABCD中,AD∥BC,∠C=90°,∠B=60°,AB=4,以点A为圆心在这个梯形内画出一个最大的扇形(图中阴影部分),则这个扇形的面积是4π.
如图,梯形ABCD中,AD∥BC,∠C=90°,∠B=60°,AB=4,以点A为圆心在这个梯形内画出一个最大的扇形(图中阴影部分),则这个扇形的面积是4π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:函数y=|x2-2x-3|.
已知:函数y=|x2-2x-3|.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
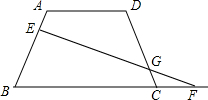 如图,已知在梯形ABCD中,AD∥BC,AD=AB=CD=5,∠ABC=60°,E是AB边上一点,AE:BE=2:3,点F是射线BC上一点,联结EF交射线DC于点G,
如图,已知在梯形ABCD中,AD∥BC,AD=AB=CD=5,∠ABC=60°,E是AB边上一点,AE:BE=2:3,点F是射线BC上一点,联结EF交射线DC于点G,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
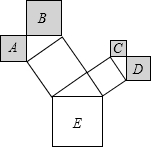 如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的边长分别是2,3,1,2,则最大正方形E的面积是18.
如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的边长分别是2,3,1,2,则最大正方形E的面积是18.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
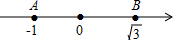 如图,数轴上A、B两点,表示的数分别为-1和$\sqrt{3}$,点B关于点A的对称点为C,点C所表示的实数是-2-$\sqrt{3}$.
如图,数轴上A、B两点,表示的数分别为-1和$\sqrt{3}$,点B关于点A的对称点为C,点C所表示的实数是-2-$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com