
【题目】已知点![]() 为双曲线
为双曲线![]() 上的一点,过点
上的一点,过点![]() 作
作![]() 轴、
轴、![]() 轴的垂线,分别交直线
轴的垂线,分别交直线![]() 于点
于点![]() 、
、![]() 两点(点
两点(点![]() 在点
在点![]() 下方.若直线
下方.若直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,则
,则![]() 的值为________.
的值为________.
【答案】![]()
【解析】
作CE⊥x轴于E,DF⊥y轴于F,由直线的解析式为y=-x+m,易得A(0,m),B(m,0),得到△OAB等腰直角三角形,则△ADF和△CEB都是等腰直角三角形,设M的坐标为(a,b),则ab=![]() ,并且CE=b,DF=a,则AD=
,并且CE=b,DF=a,则AD=![]() DF=
DF=![]() a,BC=
a,BC=![]() ,CE=
,CE=![]() b,于是得到ADBC=
b,于是得到ADBC=![]() a
a![]() b=2ab=
b=2ab=![]() .
.
作CE⊥x轴于E,DF⊥y轴于F,如图,
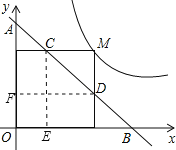
对于y=-x+m,
令x=0,则y=m;令y=0,-x+m=0,解得x=m,
∴A(0,m),B(m,0),
∴△OAB等腰直角三角形,
∴△ADF和△CEB都是等腰直角三角形,
设M的坐标为(a,b),则ab=![]() ,
,
CE=b,DF=a,
∴AD=![]() DF=
DF=![]() a,BC=
a,BC=![]() CE=
CE=![]() b,
b,
∴ADBC=![]() b
b![]()
![]() a=2ab=2
a=2ab=2![]() .
.
故答案为:2![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某种蔬菜的销售单价y1与销售月份x之间的关系如图1所示,成本y2与销售月份x之间的关系如图2所示(图1的图象是线段,图2的图象是抛物线)
(1)已知6月份这种蔬菜的成本最低,此时出售每千克的收益是多少元?(收益=售价﹣成本)
(2)哪个月出售这种蔬菜,每千克的收益最大?简单说明理由.
(3)已知市场部销售该种蔬菜4、5两个月的总收益为22万元,且5月份的销售量比4月份的销售量多2万千克,求4、5两个月的销售量分别是多少万千克?
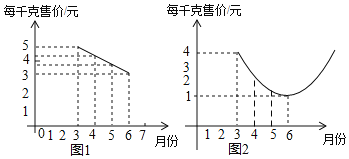
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】教材呈现:下图是华师版八年级下册数学教材第11页的部分内容.
例1,如图,在菱形![]() 中,
中,![]() ,试求
,试求![]() 的大小,并说明
的大小,并说明![]() 是等边三角形
是等边三角形
问题解决:请结合图(1),写出例1的完整解答过程;

问题探究:在菱形![]() 中,对角线
中,对角线![]() 相交于点
相交于点![]() ,过点D作
,过点D作![]() 交BC的延长线于点E.
交BC的延长线于点E.
(1)如图2,连接OE,则OE的长为____________;
(2)如图3,若点P是对角线BD上一动点,连结![]() ,则
,则![]() 的最小值为____________.
的最小值为____________.
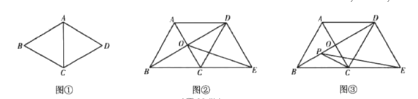
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△![]() 中,高
中,高![]() =3,∠
=3,∠![]() =45°,
=45°,![]() =
=![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向以每秒1个单位长度的速速向终点
方向以每秒1个单位长度的速速向终点![]() 运动,当点
运动,当点![]() 与点
与点![]() 、
、![]() 不重合时,过点
不重合时,过点![]() 作
作![]() 、
、![]() 的平行线,与
的平行线,与![]() 分别交于点
分别交于点![]() 、
、![]() ,将△
,将△![]() 绕
绕![]() 的中点旋转180°得△
的中点旋转180°得△![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() 秒,△
秒,△![]() 与△
与△![]() 重叠部分面积为
重叠部分面积为![]() .
.
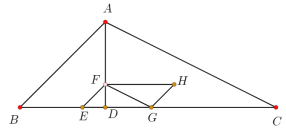
(1)当![]() = 秒时,点
= 秒时,点![]() 落在
落在![]() 边上.
边上.
(2)求![]() 与
与![]() 的函数关系式.
的函数关系式.
(3)当直线![]() 将△
将△![]() 分为面积比为1:3的两部分时,直接写出
分为面积比为1:3的两部分时,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
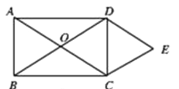
【题目】矩形ABCD的对角线相交于点O.DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠ACB=30°,菱形OCED的而积为![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点B的坐标为(1,0)其图象如图所示,下列结论:①abc>0;②2a﹣b=0;③一元二次方程ax2+bx+c=0的两个根是﹣3和1;④当y>0时,﹣3<x<1;⑤当x>0时,y随x的增大而增大:⑥若点E(﹣4,y1),F(﹣2,y2),M(3,y3)是函数图象上的三点,则y1>y2>y3,其中正确的有( )个
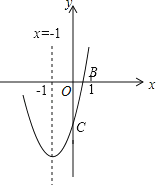
A.5B.4C.3D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小微企业为加快产业转型升级步伐,引进一批A,B两种型号的机器.已知一台A型机器比一台B型机器每小时多加工2个零件,且一台A型机器加工80个零件与一台B型机器加工60个零件所用时间相等.
(1)每台A,B两种型号的机器每小时分别加工多少个零件?
(2)如果该企业计划安排A,B两种型号的机器共10台一起加工一批该零件,为了如期完成任务,要求两种机器每小时加工的零件不少于72件,同时为了保障机器的正常运转,两种机器每小时加工的零件不能超过76件,那么A,B两种型号的机器可以各安排多少台?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:
如图所示,有三根针和套在一根针上的若干金属片,按下列规则,把金属片从一根针上全部移到另一根针上.

a.每次只能移动1个金属片;
b.较大的金属片不能放在较小的金属片上面.
把![]() 个金属片从1号针移到3号针,最少移动多少次?
个金属片从1号针移到3号针,最少移动多少次?
问题探究:为了探究规律,我们采用一般问题特殊化的方法,先从简单的情形入手,再逐次递进,最后得出一般性结论.
探究一:当![]() 时,只需把金属片从1号针移到3号针,用符号
时,只需把金属片从1号针移到3号针,用符号![]() 表示,共移动了1次.
表示,共移动了1次.
探究二:当![]() 时,为了避免将较大的金属片放在较小的金属片上面,我们利用2号针作为“中间针”,移动的顺序是:
时,为了避免将较大的金属片放在较小的金属片上面,我们利用2号针作为“中间针”,移动的顺序是:
a.把第1个金属片从1号针移到2号针;
b.把第2个金属片从1号针移到3号针;
c.把第1个金属片从2号针移到3号针.
用符号表示为:![]() ,
,![]() ,
,![]() .共移动了3次.
.共移动了3次.
探究三:当![]() 时,把上面两个金属片作为一个整体,则归结为
时,把上面两个金属片作为一个整体,则归结为![]() 的情形,移动的顺序是:
的情形,移动的顺序是:
a.把上面两个金属片从1号针移到2号针;
b.把第3个金属片从1号针移到3号针;
c.把上面两个金属片从2号针移到3号针.
其中(1)和(3)都需要借助中间针,用符号表示为:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .共移动了7次.
.共移动了7次.
(1)探究四:请仿照前面步骤进行解答:当![]() 时,把上面3个金属片作为一个整体,移动的顺序是:___________________________________________________.
时,把上面3个金属片作为一个整体,移动的顺序是:___________________________________________________.
(2)探究五:根据上面的规律你可以发现当![]() 时,需要移动________次.
时,需要移动________次.
(3)探究六:把![]() 个金属片从1号针移到3号针,最少移动________次.
个金属片从1号针移到3号针,最少移动________次.
(4)探究七:如果我们把![]() 个金属片从1号针移到3号针,最少移动的次数记为
个金属片从1号针移到3号针,最少移动的次数记为![]() ,当
,当![]() 时如果我们把
时如果我们把![]() 个金属片从1号针移到3号针,最少移动的次数记为
个金属片从1号针移到3号针,最少移动的次数记为![]() ,那么
,那么![]() 与
与![]() 的关系是
的关系是![]() __________.
__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抗击新冠肺炎期间,某小区为方便管理,为居民设计了一个身份识别图案系统:在4×4的正方形网格中,白色正方形表示数字1,黑色正方形表示数字0,将第i行第j列表示的数记为ai,j(其中i,j都是不大于4的正整数),例如,图1中,a1,2=0.对第i行使用公式Ai=ai,1×23+ai,2×22+ai,3×21+ai,4×20进行计算,所得结果A1,A2,A3,A4分别表示居民楼号,单元号,楼层和房间号.例如,图1中,A3=a3,1×23+a3,2×22+a3,3×21+a3,4×20=1×8+0×4+0×2+1×1=9,A4=0×8+0×4+1×2+1×1=3,说明该居民住在9层,3号房间,即903号.
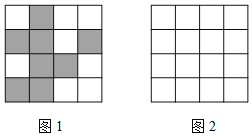
(1)图1中,a1,3= ;
(2)图1代表的居民居住在 号楼 单元;
(3)请仿照图1,在图2中画出8号楼4单元602号居民的身份识别图案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com