
【题目】阅读下列材料:
问题:如图1,在△![]() 中,点
中,点![]() 为
为![]() 的中点,求证:
的中点,求证: ![]() <
<![]() 小明提供了他研究这个问题的思路:从点
小明提供了他研究这个问题的思路:从点![]() 为
为![]() 的中点出发,可以构造以
的中点出发,可以构造以![]() 、
、![]() 为邻边的平行四边形
为邻边的平行四边形![]() ,结合平行四边形的性质以及三角形两边之和大于第三边的性质便可解决这个问题.请结合小明研究问题的思路,解决下列问题:
,结合平行四边形的性质以及三角形两边之和大于第三边的性质便可解决这个问题.请结合小明研究问题的思路,解决下列问题:
(1)完成上面问题的解答;
(2)如果在图1中,∠![]() =60°,延长
=60°,延长![]() 到
到![]() ,使得
,使得![]() ,延长
,延长![]() 到
到![]() ,使得
,使得![]() ,连结
,连结![]() ,如图2. 请猜想线段
,如图2. 请猜想线段![]() 与线段
与线段![]() 之间的数量关系.并加以证明.
之间的数量关系.并加以证明.
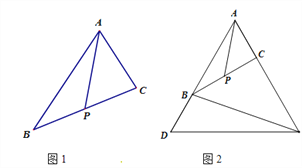
【答案】(1)证明见解析;(2)BE=2AP,证明见解析
【解析】试题分析:(1)可通过构建平行四边形求解;延长AP至H,使PH=AP;则AH、BC互相平分,四边形ABHC是平行四边形;在△ACH中,由三角形三边关系定理知:AH<AC+CH,而HC=AB,AH=2AP,等量代换后即可证得所求的结论;
(2)可按照(1)题的思路求解;过B作AE的平行线,交DE于H,连接AH、CH;易知AD=AE,若∠BAC=60°,则△ADE是等边三角形,易证得△DBH也是等边三角形,此时DB=BH=AC,则四边形ABHC的一组对边平行且相等,则四边形ABHC是平行四边形;由此可证得P是平行四边形ABHC对角线的交点,且AH=2AP;下面可通过证△DBE≌△DHA得出AH=DE,从而得出DE=2AP的结论;
试题解析:
(1)证明:延长AP至H,使得PH=AP,连接BH、HC,PH;
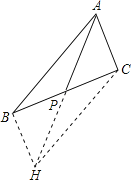
∵BP=PC;
∴四边形ABHC是平行四边形;
∴AB=HC;
在△ACH中,AH<HC+AC;
∴2AP<AB+AC;
即AP<![]() (AB+AC)
(AB+AC)
(2) BE=2AP.
证明:过B作BH∥AE交DE于H,连接CH、AH;
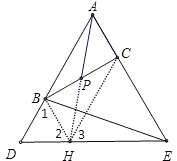
∴∠1=∠BAC=60°;
∵DB=AC,AB=CE,
∴AD=AE,
∴△AED是等边三角形,
∴∠D=∠1=∠2=∠AED=60°;
∴△BDH是等边三角形;
∴BD=DH=BH=AC;
∴四边形ABHC是平行四边形;
∵点P是BC的中点,
∴点P是四边形ABHC对角线AH、BC的交点,
∴点A,P,H共线,
∴AH=2AP;
在△ADH和△EDB中, 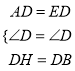 ;
;
∴△ADH≌△EDB;
∴AH=BE=2AP;


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】某次数学测验,共16个选择题,评分标准为:;对一题给6分,错一题扣2分,不答不给分。某个学生有1题未答,他想自己的分数不低于70分,他至少要对多少题?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】试解答下列问题:
(1)在图1我们称之为“8字形”,请直接写出∠A、∠B、∠C、∠D之间的数量关系: ;
(2)仔细观察,在图2中“8字形”的个数是 个;
(3) 在图2中,若∠D=40°,∠B=36°,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试求∠P的度数;
(4)如果图2中∠D和∠B为任意角时,其他条件不变,试写出∠B与∠P、∠D之间数量关系 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某学校七至九年级学生每天的体育锻炼时间,下列抽样调查的样本代表性较好的是
A. 选择七年级一个班进行调查
B. 选择八年级全体学生进行调查
C. 选择全校七至九年级学号是5的整数倍的学生进行调查
D. 对九年级每个班按5%的比例用抽签的方法确定调查者
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】调查某班级的学生对数学老师的喜欢程度,下列最具有代表性的样本是( )
A. 调查单数学号的学生 B. 调查所有的班级干部
C. 调查全体女生 D. 调查数学兴趣小组的学生
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视机厂生产甲、乙、丙三种不同型号的电视机,出厂价分别为1200元,2000元,2200元.某商场同时从该厂购进其中两种不同型号的电视机共50台,正好用去80000元.
(1)该商场有几种进货方案?(写出演算步骤)
(2)若该商场销售甲、乙、丙种电视机每台可分别获利200元,250元,300元,如何进货可使销售时获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在一次扶贫助残活动中,共捐款5280000元,将5280000用科学记数法表示为( )
A. 5.28×106 B. 5.28×107
C. 52.8×106 D. 0.528×107
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com