
如图,AC是圆O的直径,AC=10厘米,PA,PB是圆O的切线,A,B为切点,过A作AD⊥BP,交BP于D点,连结AB、BC.
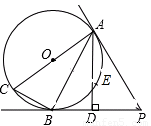
(1)求证△ABC∽△ADB;
(2)若切线AP的长为12厘米,求弦AB的长.
(1)证明:∵AC是圆O的直径,∴∠ABC=90 o,
又∵AD⊥BP,∴∠ADB=90 o,∴∠ABC=∠ADB,
又∵PB是圆的切线,∴∠ABD=∠ACB,
在△ABC和△ADB中:
 ,∴△ABC∽△ADB;
,∴△ABC∽△ADB;
(2)如图,连结OP,

在Rt△AOP中,AP=12厘米,OA=5厘米,根据勾股定理求得OP=13厘米,
又由已知可证得△ABC∽△PAO, ∴ ,得
,得 ,解得AB=
,解得AB= 厘米.
厘米.
【解析】(1)根据AC为⊙O的半径,可知:∠ABC=90°,由AD⊥BP,可知:∠ABC=∠ADB,根据切线的性质知:∠ABD=∠ACB,从而可证:△ABC∽△ADB;
(2)在Rt△POA中,根据勾股定理可将OP的长求出,再根据△ABC∽△PAO,可将AB的长求出.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 D点,连接AB,BC.
D点,连接AB,BC.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,AC是圆O的直径,PA切圆O于点A,弦BC∥OP,OP交圆O于点D,连接PB
如图,AC是圆O的直径,PA切圆O于点A,弦BC∥OP,OP交圆O于点D,连接PB查看答案和解析>>
科目:初中数学 来源:2008年初中毕业升学考试(山东潍坊卷)数学(带解析) 题型:解答题
如图,AC是圆O的直径,AC=10厘米,PA,PB是圆O的切线,A,B为切点,过A作AD⊥BP,交BP于D点,连结AB、BC.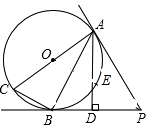
(1)求证△ABC∽△ADB;
(2)若切线AP的长为12厘米,求弦AB的长.
查看答案和解析>>
科目:初中数学 来源:第5章《中心对称图形(二)》中考题集(34):5.5 直线与圆的位置关系(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com