
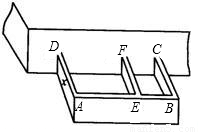
某农户计划利用现有的一面墙(墙长8米),再修四面墙,建造如图所示的长方体水池,培育不同品种的鱼苗.他已备足可以修高为1.5m、长18m的墙的材料准备施工,设图中与现有一面墙垂直的三面墙的长度都为xm,即AD=EF=BC=xm.(不考虑墙的厚度).

(1)若想水池的总容积为36m3,x应等于多少?
(2)求水池的总容积V与x的函数关系式,并直接写出x的取值范围;
(3)若想使水池的总容积V最大,x应为多少?最大容积是多少?
(1)2或4;(2) ,x的取值范围是
,x的取值范围是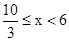 ;(3)当
;(3)当 时,总容积V最大=40.
时,总容积V最大=40.
【解析】
试题分析:(1)这个水槽是个长方体,我们先看这个矩形的面积,有了AD、EF、BC的长,因为材料的总长度是18m,因此这个矩形的长应该是18﹣3x,又知道宽为x,又已知了长方体的高,因此可根据长×宽×高=36m3来得出关于x的二次方程从而求出x的值.
(2)和(1)类似,只需把36立方米换成V即可.
(3)此题是求二次函数的最值,可以用配方法或公式法,来求出此时x、y的值.
试题解析:(1)∵AD=EF=BC=x,∴AB=18﹣3x,∴水池的总容积为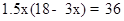 ,即
,即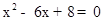 ,解得:x=2或4,所以x应为2m或4m;
,解得:x=2或4,所以x应为2m或4m;
(2)由(1)知V与x的函数关系式为: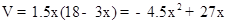 ,∵AB≤8,∴18-3x≤8,解得x≥
,∵AB≤8,∴18-3x≤8,解得x≥ ,x的取值范围是:
,x的取值范围是: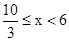 ;
;
(3) ,∴由函数图象知:当x=3时,V有最大值40.5.∵
,∴由函数图象知:当x=3时,V有最大值40.5.∵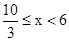 ,∴若使水池的总容积最大,
,∴若使水池的总容积最大, ,最大容积为40m3.
,最大容积为40m3.
考点:1.二次函数的应用;2.应用题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
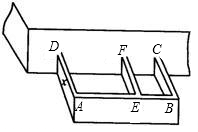 墙垂直的三面墙的长度都为xm,即AD=EF=BC=xm.(不考虑墙的厚度)
墙垂直的三面墙的长度都为xm,即AD=EF=BC=xm.(不考虑墙的厚度)查看答案和解析>>
科目:初中数学 来源:《第26章 二次函数》2010年复习题(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:第6章《二次函数》常考题集(18):6.4 二次函数的应用(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2011年1月浙江省杭州市滨江区九年级(上)月考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com