
 如图,在Rt△ABO中,顶点A(横坐标为1)是双曲线y=$\frac{k}{x}$与直线y=-x+(k+1)在第四象限的交点,AB⊥x轴于B且S△ABO=$\frac{3}{2}$.
如图,在Rt△ABO中,顶点A(横坐标为1)是双曲线y=$\frac{k}{x}$与直线y=-x+(k+1)在第四象限的交点,AB⊥x轴于B且S△ABO=$\frac{3}{2}$. 分析 (1)由S△ABO=$\frac{3}{2}$,根据反比例函数的系数k的几何意义,即可求出k的值,从而求得两个函数的解析式;
(2)将两函数解析式组成方程组,求出方程组的解即为交点坐标,求出直线AC和x轴的交点坐标,结合A、C的坐标,利用三角形的面积公式即可求出S△AOC.
解答  解:(1)∵S△ABO=$\frac{3}{2}$,
解:(1)∵S△ABO=$\frac{3}{2}$,
∴|k|=2×$\frac{3}{2}$=3,
由于反比例函数的图象位于二、四象限,
∴k=-3,
∴反比例函数解析式为y=-$\frac{3}{x}$.
一次函数解析式为y=-x-3+1,
即y=-x-2.
(2) 解$\left\{\begin{array}{l}{y=-\frac{3}{x}}\\{y=-x-2}\end{array}\right.$得$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=3}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-3}\\{{y}_{2}=1}\end{array}\right.$.
解$\left\{\begin{array}{l}{y=-\frac{3}{x}}\\{y=-x-2}\end{array}\right.$得$\left\{\begin{array}{l}{{x}_{1}=1}\\{{y}_{1}=3}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-3}\\{{y}_{2}=1}\end{array}\right.$.
∴A(1,-3),C(-3,1).
设直线与x轴的交点为D,令y=0,则有-x-2=0,
解得x=-2,故D点坐标为(-2,0).
∴S△AOC=S△DOC+S△AOD
=$\frac{1}{2}$×2×1+$\frac{1}{2}$×2×3
=1+3
=4.
点评 此题首先利用待定系数法确定函数解析式,然后利用解方程组来确定图象的交点坐标,及利用坐标求出线段和图形的面积.


科目:初中数学 来源: 题型:选择题
| A. | 1.83×106 | B. | 1.83×107 | C. | 1.83×108 | D. | 1.83×109 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
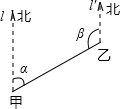 如图,在甲、乙两地之间要修一条公路,从甲地测得公路的走向是北偏东55°,如果甲、乙两地同时开工,要使公路准确接通,那么在乙地公路施工时∠β的度数应该为( )
如图,在甲、乙两地之间要修一条公路,从甲地测得公路的走向是北偏东55°,如果甲、乙两地同时开工,要使公路准确接通,那么在乙地公路施工时∠β的度数应该为( )| A. | 135° | B. | 125° | C. | 55° | D. | 35° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com