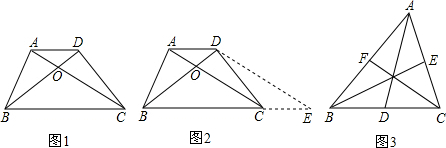
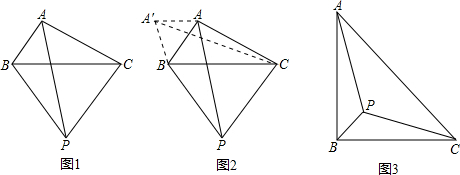
解:阅读材料:
∵△ADE绕点A顺时针旋转90°得到△ABG,
∴∠GAB=∠EAD,
∵四边形ABCD是正方形,
∴∠BAD=90°,
∵∠EAF=45°,
∴∠GAF=∠GAB+∠BAF,
=∠EAD+∠BAF,
=∠BAD-∠EAF,
=90°-45°,
=45°;
(1)如图3,过点A作AF⊥CB交CB的延长线于点F,
∵AD∥BC,∠D=90°,AD=CD,
∴四边形AFCD是正方形,
设BE=x,
根据小伟的结论,BF=BE-DE=x-4,
∵CD=10,DE=4,
∴CE=CD-DE=10-4=6,
BC=CF-BF=10-(x-4)=14-x,
在Rt△BCE中,BC
2+CE
2=BE
2,
即(14-x)
2+6
2=x
2,
整理得,-28x=-232,
解得x=
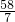
,
即BE=
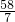
;
(2)如图4,过点A作AE⊥x轴于E,过点C作CF⊥x轴于F,
在正方形ABCD中,AB=BC,∠ABC=90°,

∵∠ABE+∠CBF=180°-90°=90°,
∠ABE+∠BAE=90°,
∴∠BAE=∠CBF,
在△ABE和△BCF中,
∵

,
∴△ABE≌△BCF(AAS),
∴AE=BF,BE=CF,
∵点A(-3,2),C(x,y),
∴OE=3,AE=2,OF=x,CF=y,
∴OB=BE-OE=y-3,
OB=OF-BF=x-2,
∴y-3=x-2,
整理得,y=x+1.
故答案为:45°;
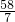
;x+1.
分析:阅读材料:根据旋转只改变图形的位置不改变图形的形状与大小可得∠GAB=∠EAD,然后求出∠GAF=∠BAF+∠EAD,再根据∠EAF=45°计算即可得解;
(1)过点A作AF⊥CB交CB的延长线于点F,可得四边形AFCD是正方形,然后设BE=x,根据小伟的结论表示出BF,再求出CE、BC,然后在Rt△BCE中,利用勾股定理列式进行计算即可得解;
(2)过点A作AE⊥x轴于E,过点C作CF⊥x轴于F,然后利用“AAS”证明△ABE和△BCF全等,根据全等三角形对应边相等可得AE=BF,BE=CF,再根据点A、C的坐标表示出OB,整理即可得解.
点评:本题考查了旋转的性质,坐标与图形的性质,全等三角形的判定与性质,正方形的性质,(2)作辅助线补充完整正方形是解题的关键,(3)作辅助线构造全等三角形是解题的关键.


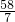 ,
,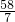 ;
;
 ,
,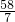 ;x+1.
;x+1.

 综合自测系列答案
综合自测系列答案