
【题目】城区某新建住宅小区计划购买并种植甲、乙两种树苗共300株.已知甲种树苗每株60元,乙种树苗每株90元.
(1)若购买树苗共用21000元,问甲、乙两种树苗应各买多少株?
(2)据统计,甲、乙两种树苗每株树苗对空气的净化指数分别为![]() 和
和![]() ,问如何购买甲、乙两种树苗才能保证该小区的空气净化指数之和等于90?
,问如何购买甲、乙两种树苗才能保证该小区的空气净化指数之和等于90?
【答案】(1)甲种树苗买200株,则乙种树苗买100株;(2)应买225株甲种树苗,75株乙种树苗时该小区的空气净华指数之和不低于90,费用最小为20250元.
【解析】
(1)设甲种树苗买x株,则乙种树苗买(300-x)株,根据“甲树苗的费用+乙树苗的费用=21000”作为相等关系列方程即可求解;
(2)设买x株甲种树苗,(300-x)株乙种树苗时该小区的空气净化指数之和不低于90,先根据“空气净化指数之和不低于90”列不等式求得x的取值范围,再根据题意用x表示出费用,列成一次函数的形式,利用一次函数的单调性来讨论费用的最小值,即函数最小值问题.
(1)设甲种树苗买x株,则乙种树苗买(300-x)株
60x+90(300-x)=21000
x=200
300-200=100
答:甲种树苗买200株,则乙种树苗买100株.
(2)设买x株甲种树苗,(300-x)株乙种树苗时该小区的空气净华指数之和不低于90
0.2x+0.6(300-x)≥90
0.2x+180-0.6x≥90
-0.4x≥-90
x≤225
此时费用y=60x+90(300-x)
y=-30x+27000
∵y是x的一次函数,y随x的增大而减少
∴当x最大=225时,y最小=-30×225+27000=20250(元)
即应买225株甲种树苗,75株乙种树苗时该小区的空气净华指数之和不低于90,费用最小为20250元.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB,FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=7,BE=2,求半圆和菱形ABFC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若任意一个代数式,在给定的范围内求得的最值恰好也在该范围内,则称这个代数式是这个范围的“友好代数式”.例如:关于![]() 的代数式
的代数式![]() ,当
,当![]() 时,代数式
时,代数式![]() 在
在![]() 时有最大值,最大值为1;在
时有最大值,最大值为1;在![]() 时有最小值,最小值为0,此时最值1,0均在
时有最小值,最小值为0,此时最值1,0均在![]() (含端点)这个范围内,则称代数式
(含端点)这个范围内,则称代数式![]() 是
是![]() 的“友好代数式”.
的“友好代数式”.
(1)若关于![]() 的代数式
的代数式![]() ,当
,当![]() 时,取得的最大值为________;最小值为________;代数式
时,取得的最大值为________;最小值为________;代数式![]() ________(填“是”或“不是”)
________(填“是”或“不是”)![]() 的“友好代数式”;
的“友好代数式”;
(2)以下关于![]() 的代数式,是
的代数式,是![]() 的“友好代数式”的是________;
的“友好代数式”的是________;
①![]() ;②
;②![]() ;③
;③![]() ;
;
(3)若关于![]() 的代数式
的代数式![]() 是
是![]() 的“友好代数式”,则
的“友好代数式”,则![]() 的值是________;
的值是________;
(4)若关于![]() 的代数式
的代数式![]() 是
是![]() 的“友好代数式”,求
的“友好代数式”,求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,AB=1,∠A=60°,∠ABC=90°,如图所示将Rt△ABC沿直线l无滑动地滚动至Rt△DEF,则点B所经过的路径与直线l所围成的封闭图形的面积为_____.(结果不取近似值)
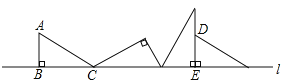
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋中装有4个红球,3个白球,2个黄球,每个球除颜色外都相同.
(1)请判断下列事件是不确定事件、不可能事件还是必然事件,填写在横线上.
①从口袋中任意摸出1个球是白球;
②从口袋中任意摸出4个球全是白球;
③从口袋中任意摸出1个球是红球或黄球;
④从口袋中任意摸出8个球,红、白、黄三种颜色的球都有;
(2)请求出(1)中不确定事件的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC为等边三角形,点D,E为直线BC上两动点,且BD=CE. 点F,点E关于直线AC成轴对称,连接AE,顺次连接A,D,F.
(1)如图1,若点D,点E在边BC上,试判断△ADF的形状并说明理由;
(2)如图2,若点D,点E在边BC外,求证:![]() .
.
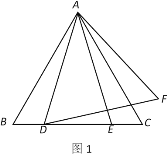
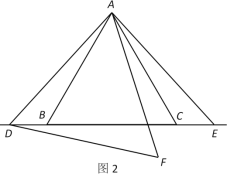
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A7B7A8的边长为( )
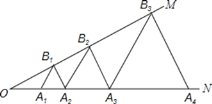
A. 64B. 32C. 16D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
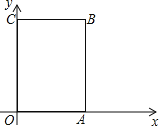
【题目】如图,长方形OABC中,O为平面直角坐标系的原点,A点的坐标为(4,0),C点的坐标为(0,5),点B在第一象限内,点P从原点出发,以每秒2个单位长度的速度沿着O﹣C﹣B﹣A﹣O的路线移动(即:沿着长方形移动一周)
(1)写出点B的坐标( , );
(2)当点P移动了4秒时,描出此时P点的位置,并求出点P的坐标;
(3)在移动过程中,当点P到x轴距离为4个单位长度时,求点P移动的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E,F为BC上两点,且BE=CF,连接AF,DE交于点O.求证:
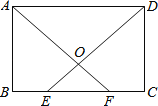
(1)△ABF≌△DCE;
(2)△AOD是等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com