
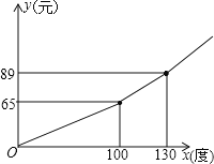
”¾ĢāÄæ”æµēĮ¦¹«Ė¾ĪŖ¹ÄĄųŹŠĆń½ŚŌ¼ÓƵē£¬²ÉČ”°“ŌĀÓƵēĮæ·Ö¶ĪŹÕ·Ń°ģ·Ø£®Čōij»§¾ÓĆńĆæŌĀÓ¦½»µē·Ńy£ØŌŖ£©ÓėÓƵēĮæx£Ø¶Č£©µÄŗÆŹżĶ¼ĻóŹĒŅ»ĢõÕŪĻߣØČēĶ¼ĖłŹ¾£©£¬øł¾ŻĶ¼Ļó½āĻĀĮŠĪŹĢā£ŗ
(1) ·Ö±šŠ“³öµ±0”Üx”Ü100ŗĶx£¾100Ź±£¬yÓėxµÄŗÆŹż¹ŲĻµŹ½
(2) ĄūÓĆŗÆŹż¹ŲĻµŹ½£¬ĖµĆ÷µēĮ¦¹«Ė¾²ÉČ”µÄŹÕ·Ń±ź×¼
(3) ČōøĆÓĆ»§Ä³ŌĀÓƵē62¶Č£¬ŌņÓ¦½É·Ń¶ąÉŁŌŖ£æČōøĆÓĆ»§Ä³ŌĀ½É·Ń105ŌŖŹ±£¬ŌņøĆÓĆ»§øĆŌĀÓĆĮĖ¶ąÉŁ¶Čµē£æ
”¾“š°ø”æ£Ø£±£©![]()
£Ø£²£©ÓĆ»§ŌĀÓƵēĮæŌŚ£°¶Čµ½100¶ČÖ®¼äŹ±£¬Ćæ¶ČµēµÄŹÕ·Ń±ź×¼ŹĒ0.65ŌŖ£¬³¬³ö100¶ČŹ±£¬Ćæ¶ČµēµÄŹÕ·Ń±ź×¼ŹĒ0.80ŌŖ£®
£Ø£³£©ÓĆ»§ÓƵē62¶ČŹ±£¬ÓĆ»§Ó¦½É·Ń40. 3ŌŖ£¬ČōÓĆ»§ŌĀ½É·Ń105ŌŖŹ±£¬øĆÓĆ»§øĆŌĀÓĆĮĖ150¶Čµē£®
”¾½āĪö”æ
ŹŌĢāÓÉĶ¼ĻóæÉÖŖ£¬µ±0”Üx”Ü100Ź±£¬æÉÉčøĆÕż±ČĄżŗÆŹż½āĪöŹ½ĪŖy=kx£¬µ±x£¾100Ź±£¬æÉÉčøĆŅ»“ĪŗÆŹż½āĪöŹ½ĪŖy=kx+b£¬½ų¶ųĄūÓĆ“ż¶ØĻµŹż·ØĒó³öŗÆŹż±ķ“ļŹ½£»
øł¾ŻĶ¼Ļó£¬ŌĀÓƵēĮæŌŚ0¶Čµ½100¶ČÖ®¼äŹ±£¬Ēó³öĆæ¶ČµēµÄŹÕ·ŃµÄ±ź×¼£¬ŌĀÓƵēĮ泬³ö100¶ČŹ±£¬Ēó³öĆæ¶ČµēµÄŹÕ·Ń±ź×¼£»
ĻČøł¾Ż×Ō±äĮæµÄֵȷ¶Ø³ö¶ŌÓ¦µÄŗÆŹż±ķ“ļŹ½£¬ŌŁ“śČėĒóÖ¤¼“æÉ.
ŹŌĢā½āĪö£ŗ£Ø1£©Éčµ±0”Üx”Ü100Ź±£¬ŗÆŹż½āĪöŹ½ĪŖy=kx£Øk”Ł0£©.
½«£Ø100£¬65£©“śČėy=kxµĆ£ŗ100k=65£¬½āµĆk=0.65£®
Ōņy=0.65x£Ø0”Üx”Ü100£©.
Éčµ±x£¾100Ź±£¬ŗÆŹż½āĪöŹ½ĪŖy=ax+b£Øa”Ł0£©.
½«£Ø100£¬65£©£¬£Ø130£¬89£©“śČėy=kx+bµĆ£ŗ
![]() £¬½āµĆ£ŗ
£¬½āµĆ£ŗ![]() £®Ōņy=0.8x-15£Øx£¾100£©
£®Ōņy=0.8x-15£Øx£¾100£©
ĖłŅŌyÓėxµÄŗÆŹż¹ŲĻµŹ½ĪŖ![]() £»
£»
£Ø2£©øł¾Ż£Ø1£©µÄŗÆŹż¹ŲĻµŹ½µĆ£ŗ
ŌĀÓƵēĮæŌŚ0¶Čµ½100¶ČÖ®¼äŹ±£¬Ćæ¶ČµēµÄŹÕ·ŃµÄ±ź×¼ŹĒ0.65ŌŖ£»ŌĀÓƵēĮ泬³ö100¶ČŹ±£¬Ćæ¶ČµēµÄŹÕ·Ń±ź×¼ŹĒ0.8ŌŖ£»
£Ø3£©ÓĆ»§ŌĀÓƵē62¶ČŹ±£¬62”Į0.65=40.3£¬ÓĆ»§Ó¦½É·Ń40.3ŌŖ£¬
ÓĆ»§ŌĀ½É·Ń105ŌŖŹ±£¬¼“0.8x-15=105£¬½āµĆx=150£¬øĆÓĆ»§øĆŌĀÓĆĮĖ150¶Čµē.


 ÓĄĒ¬½ĢÓżŗ®¼Ł×÷ŅµæģĄÖ¼ŁĘŚŃÓ±ßČĖĆń³ö°ęÉēĻµĮŠ“š°ø
ÓĄĒ¬½ĢÓżŗ®¼Ł×÷ŅµæģĄÖ¼ŁĘŚŃÓ±ßČĖĆń³ö°ęÉēĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼×”¢ŅŅĮ½¼ŅÉĢµź³öŹŪĶ¬ŃłÅĘ×ÓŗĶ¹ęøńµÄӚƫĒņÅÄŗĶӚƫĒņ£¬Ćæø±ĒņÅĶؼŪ300ŌŖ£¬ĆæŗŠÓšĆ«Ēņ¶Ø¼Ū40ŌŖ£¬ĪŖĒģ×£ĪåŅ»½Ś£¬Į½¼ŅÉĢµźæŖÕ¹“ŁĻś»ī¶ÆČēĻĀ£ŗ
¼×ÉĢµź£ŗĖłÓŠÉĢĘ·9ÕŪÓÅ»Ż£»
ŅŅÉĢµź£ŗĆæĀņ1ø±ĒņÅÄŌłĖĶ1ŗŠÓšĆ«Ēņ”£
ijŠ£ÓšĆ«Ēņ¶ÓŠčŅŖ¹ŗĀņ![]() ø±ĒņÅÄŗĶ
ø±ĒņÅÄŗĶ![]() ŗŠÓšĆ«Ēņ
ŗŠÓšĆ«Ēņ![]() .
.
(1)°“ÉĻŹöµÄ“ŁĻś·½Ź½£¬øĆŠ£ÓšĆ«Ēņ¶ÓŌŚ¼×”¢ŅŅĮ½¼ŅÉĢµźø÷Ó¦»Ø·Ń¶ąÉŁŌŖ?ŹŌÓĆŗ¬![]() ”¢
”¢![]() µÄ“śŹżŹ½±ķŹ¾£»
µÄ“śŹżŹ½±ķŹ¾£»
(2)µ±![]() Ź±£¬ŹŌÅŠ¶Ļ·Ö±šµ½¼×”¢ŅŅĮ½¼ŅÉĢµź¹ŗĀņĒņÅÄŗĶӚƫĒņ£¬ÄļŅ±ćŅĖ?
Ź±£¬ŹŌÅŠ¶Ļ·Ö±šµ½¼×”¢ŅŅĮ½¼ŅÉĢµź¹ŗĀņĒņÅÄŗĶӚƫĒņ£¬ÄļŅ±ćŅĖ?
(3)µ±![]() ”¢
”¢![]() Āś×ćŹ²Ć“¹ŲĻµŹ±£¬µ½¼×”¢ŅŅĮ½¼ŅÉĢµź¹ŗĀņĒņÅÄŗĶӚƫĒņµÄ·ŃÓĆĻąĶ¬?
Āś×ćŹ²Ć“¹ŲĻµŹ±£¬µ½¼×”¢ŅŅĮ½¼ŅÉĢµź¹ŗĀņĒņÅÄŗĶӚƫĒņµÄ·ŃÓĆĻąĶ¬?
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijĘū³µÓĶĻäµÄČŻ»żĪŖ70Éż£¬Š”Ķõ°ŃÓĶĻä×¢ĀśÓĶŗó×¼±ø¼ŻŹ»Ęū³µ“ÓĻŲ³Ēµ½300Ē§Ć×ĶāµÄŹ”³Ē½Ó“żæĶČĖ£¬ŌŚ½Óµ½æĶČĖŗóĮ¢¼“°“ŌĀ··µ»Ų£¬Ēė»Ų“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©ÓĶĻä×¢ĀśÓĶŗó£¬Ęū³µÄܹ»ŠŠŹ¹µÄ×ÜĀ·³Ģy£Øµ„Ī»£ŗĒ§Ć×£©ÓėĘ½¾łŗÄÓĶĮæx£Øµ„Ī»£ŗÉż/Ē§Ć×£©Ö®¼äÓŠŌõŃłµÄŗÆŹż¹ŲĻµ£æ
£Ø2£©Čē¹ūŠ”ĶõŅŌĘ½¾łĆæĒ§Ć×ŗÄÓĶ0.1ÉżµÄĖŁ¶Č¼ŻŹ»Ęū³µµ½“ļŹ”³Ē£¬ŌŚ·µ³ĢŹ±ÓÉÓŚĻĀÓź£¬Š”Ķõ½µµĶĮĖ³µĖŁ£¬“ĖŹ±Ć把Ź»1Ē§Ć×µÄŗÄÓĶĮæŌö¼ÓĮĖŅ»±¶£¬Čē¹ūŠ”ĶõŅ»Ö±ŅŌ“ĖĖŁ¶ČŠŠŹ»£¬ÓŹĻäĄļµÄÓĶŹĒ·ń¹»»Ųµ½ĻŲ³Ē£æČē¹ū²»¹»ÓĆ£¬ÖĮÉŁ»¹Šč¼Ó¶ąÉŁÓĶ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ¾ŲŠĪABCDÖŠ£¬µćOŌŚ¶Ō½ĒĻßABÉĻ£¬ŅŌOAµÄ³¤ĪŖ°ė¾¶µÄŌ²OÓėAD½»ÓŚµćE£¬ĒŅ”ĻACB=”ĻDCE£¬ĒóÖ¤£ŗCEŹĒ”ŃOµÄĒŠĻߣ® 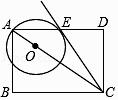
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĻĀĮŠø÷ŌĖĖćÖŠ£¬¼ĘĖćÕżČ·µÄŹĒ£Ø £©
A.£Ø©3ab2£©2=9a2b4
B.2a+3b=5ab
C.![]() =”Ą3
=”Ą3
D.£Øa©b£©2=a2©b2
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬“óÕż·½ŠĪABCDÖŠÓŠ2øöŠ”Õż·½ŠĪ£¬Čē¹ūĖüĆĒµÄĆ껿·Ö±šŹĒs1 £¬ s2 £¬ ÄĒĆ“s1s2 £® £ØĢī£¾£¬£¼»ņ=£© 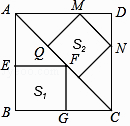
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æÓŠŅ»×éĻąĶ¬¹ęøńµÄ·¹Ķė£¬²āµĆŅ»Ö»Ķėø߶ČĪŖ4.5cm£¬Į½Ö»·¹ĶėÕūĘėµž·ÅŌŚ×ĄĆęÉĻµÄø߶ČĪŖ6.5cm£¬ČżÖ»·¹ĶėÕūĘėµž·ÅŌŚ×ĄĆęÉĻµÄø߶ČĪŖ8.5cm.øł¾ŻŅŌÉĻŠÅĻ¢»Ų“šĻĀĮŠĪŹĢā£ŗ
(1)Čō·¹ĶėŹżĪŖ![]() øö£¬ÓĆŗ¬
øö£¬ÓĆŗ¬![]() µÄ“śŹżŹ½±ķŹ¾
µÄ“śŹżŹ½±ķŹ¾![]() øö·¹ĶėÕūĘėµž·ÅŌŚ×ĄĆęÉĻµÄøß¶Č£»
øö·¹ĶėÕūĘėµž·ÅŌŚ×ĄĆęÉĻµÄøß¶Č£»
(2)µ±µž·Å·¹ĶėŹżĪŖ9øöŹ±£¬ĒóÕāµž·¹ĶėµÄø߶Č.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬µćDŹĒBA±ßŃÓ³¤ĻßÉĻŅ»µć£¬¹żµćD×÷DE”ĪBC£¬½»CAŃÓ³¤ĻßÓŚµćE£¬µćFŹĒDEŃÓ³¤ĻßÉĻŅ»µć£¬Į¬½ÓAF£® 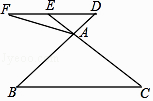
£Ø1£©Čē¹ū ![]() =
= ![]() £¬DE=6£¬Ēó±ßBCµÄ³¤£»
£¬DE=6£¬Ēó±ßBCµÄ³¤£»
£Ø2£©Čē¹ū”ĻFAE=”ĻB£¬FA=6£¬FE=4£¬ĒóDFµÄ³¤£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼ĖłŹ¾£¬ŅŃÖŖµćN£Ø1£¬0£©£¬Ö±Ļßy=©x+2ÓėĮ½×ų±źÖį·Ö±š½»ÓŚA£¬BĮ½µć£¬M£¬P·Ö±šŹĒĻ߶ĪOB£¬ABÉĻµÄ¶Æµć£¬ŌņPM+MNµÄ×īŠ”ÖµŹĒ £® 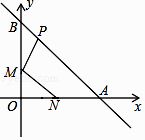
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com