
 如图,小亮在操场上玩,一段时间内沿M→A→B→M的路径匀速散步,能近似刻画小亮到出发点M的距离y与时间x之间关系的函数图象是( )
如图,小亮在操场上玩,一段时间内沿M→A→B→M的路径匀速散步,能近似刻画小亮到出发点M的距离y与时间x之间关系的函数图象是( )| A. |  | B. |  | C. |  | D. |  |
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +5 | -2 | -4 | +13 | -10 | +16 | -9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
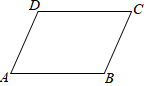 如图,AD=BC,要使四边形ABCD是平行四边形,还需补充的一个条件,下列错误的是( )
如图,AD=BC,要使四边形ABCD是平行四边形,还需补充的一个条件,下列错误的是( )| A. | AB=DC | B. | AD∥BC | C. | ∠A+∠B=180° | D. | ∠A+∠D=180° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-4)2=31 | B. | (x-4)2=1 | C. | (x-8)2=1 | D. | (x-8)2=31 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
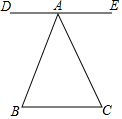 如图,ED∥BC,∠B=∠C,则下列正确的是( )
如图,ED∥BC,∠B=∠C,则下列正确的是( )| A. | ∠BAE=∠DAC | B. | ∠BAE=∠ACB | C. | ∠ABC=∠DAC | D. | ∠BAC=∠DAC |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com