
【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起(其中,![]() ,
,![]() ;
;![]() ).
).

(1)①若![]() ,则
,则![]() 的度数为_____________;
的度数为_____________;
②若![]() ,则
,则![]() 的度数为_____________.
的度数为_____________.
(2)由(1)猜想![]() 与
与![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(3)当![]() 且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出
且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请写出![]() 角度所有可能的值(不必说明理由);若不存在,请说明理由.
角度所有可能的值(不必说明理由);若不存在,请说明理由.
【答案】(1)①![]() ;②
;②![]() ;(2)
;(2)![]() ,理由详见解析;(3)∠ACE=45°或30°或120°或135°或165°
,理由详见解析;(3)∠ACE=45°或30°或120°或135°或165°
【解析】
(1)①先求出∠ACE,即可求出∠ACB;
②先求出∠ACE,即可求出∠DCE;
(2)根据题意可得![]() ,
,![]() ,从而求出
,从而求出![]() 与
与![]() 的数量关系;
的数量关系;
(3)根据平行线的判定定理和边的平行关系分类讨论,然后画出对应的图形即可得出结论.
解:(1)①∵![]() ,∠ACD=∠BCE=90°
,∠ACD=∠BCE=90°
∴∠ACE=∠ACD-∠DCE=45°
∴∠ACB=∠ACE+∠BCE=135°
故答案为:![]() .
.
②∵![]() ,∠ACD=∠BCE=90°
,∠ACD=∠BCE=90°
∴∠ACE=∠ACB-∠BCE=50°
∴∠DCE=∠ACD-∠ACE =40°
故答案为:![]() .
.
(2)![]() .理由如下
.理由如下
∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]()
∴![]() .
.
(3)①当![]() 时,
时,
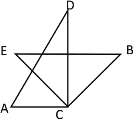
∵![]()
∴![]()
∴![]() ,
,
②当![]() 时,设CE与AD交于点F,如下图所示
时,设CE与AD交于点F,如下图所示
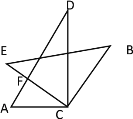
∵∠A=60°,∠BCE=90°
∴∠AFC=180°-∠ACE-∠A=90°
∴∠AFC=∠BCE
∴![]() .
.
③当![]() 时,如下图所示
时,如下图所示

∵∠ACD=90°,∠D=30°
∴∠DCE=∠ACE-∠ACD=30°
∴∠DCE=∠D
∴![]() .
.
④当![]() 时,如下图所示
时,如下图所示
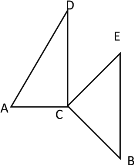
∵∠ACD=90°,∠E=45°
∴∠DCE=∠ACE-∠ACD=45°
∴∠DCE=∠E
∴![]() .
.
⑤当![]() 时,过点C作CG∥AD,如下图所示
时,过点C作CG∥AD,如下图所示
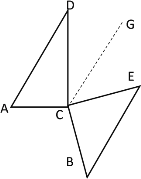
∴∠D=∠DCG=30°
∵∠ACD=90°,∠E=45°
∴∠GCE=∠ACE-∠ACD-∠DCG=45°
∴∠E=∠GCE
∴BE∥CG
∴![]() .
.
综上所述:∠ACE=45°或30°或120°或135°或165°.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】南京某中学为了迎接世乒赛,在九年级举行了“乒乓球知识竞赛”,从全年级600名学生的成绩中随机抽选了100名学生的成绩,根据测试成绩绘制成以下不完整的频数分布表和频数分布直方图:

请结合图表完成下列各题:
(1)求表中a的值:
(2)请把频数分布直方图补充完整:
(3)若测试成绩不低于90分的同学可以获得世乒赛吉祥物“乒宝”,请你估计该校九年级有多少位同学可以获得“乒宝”?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)若x,y都是实数,且y=![]() +
+![]() +8,求5x+13y+6的值;
+8,求5x+13y+6的值;
(2)已知△ABC的三边长分别为a,b,c,且满足![]() +b2-6b+9=0,求c的取值范围。
+b2-6b+9=0,求c的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线AB∥CD,BE平分∠ABC,交CD于D,∠CDE=150°,则∠C的度数为( )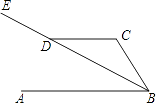
A.150°
B.130°
C.120°
D.100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请从以下两个小题中任选一题作答,若多选,则按所选的第一题计分.
A.正五边形的一个外角的度数是 .
B.比较大小:2tan71° ![]() (填“>”、“=”或“<”)
(填“>”、“=”或“<”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某服装店用1200元购进一批服装,全部售完.由于服装畅销,服装店又用2800元,购进了第二批这种服装,所购数量是第一批购进量的2倍,但单价贵了5元,仍以同样的价格出售.卖了部分后,为了加快资金周转,服装店将剩余的20件以售价的八折全部出售.
问:(1)该服装店第一次购买了此种服装多少件?
(2)如果两批服装全部售完利润率不低于16%(不考虑其它因素),那么每件服装的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】无锡市旅游局为了亮化某景点,在两条笔直且互相平行的景观道MN、QP上分别放置A、B两盏激光灯,如图所示.A灯发出的光束自AM逆时针旋转至AN便立即回转;B灯发出的光束自BP逆时针旋转至BQ便立即回转,两灯不间断照射,A灯每秒转动30°,B灯每秒转动10°.B灯先转动2秒,A灯才开始转动.当B灯光束第一次到达BQ之前,两灯的光束互相平行时A灯旋转的时间是______秒.
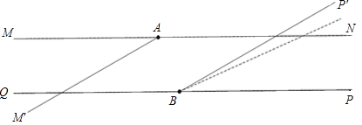
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com