
����Ŀ��ij����2014��Ͷ���������2900��Ԫ��2016��Ͷ���������3509��Ԫ��
��1����2014����2016��õ���Ͷ��������ѵ���ƽ�������ʣ�
��2����������������涨���������ѵ�Ͷ�벻���ڹ���������ֵ�İٷ�֮�ģ���ϸõ�������������ֵ������������õ�����2018����Ͷ���������4250��Ԫ���������1���н�������Ͷ��������ʣ���2018��õ���Ͷ��Ľ��������Ƿ��ܴﵽ4250��Ԫ����˵�����ɣ�
���ο����ݣ� ![]() =1.1��
=1.1�� ![]() =1.2��
=1.2�� ![]() =1.3��
=1.3�� ![]() =1.4��
=1.4��
���𰸡�
��1��
�⣺��������Ϊx����������2015��Ϊ2900��1+x����Ԫ��2016��Ϊ2900��1+x��2��Ԫ��
��2900��1+x��2=3509��
���x=0.1=10%����x=��2.1������������ȥ����
��������Ͷ��������ѵ�ƽ��������Ϊ10%
��2��
�⣺2018��õ���Ͷ��Ľ���������3509����1+10%��2=4245.89����Ԫ����
4245.89��4250��
�𣺰���1���н�������Ͷ��������ʣ���2018��õ���Ͷ��Ľ������Ѳ��ܴﵽ4250��Ԫ��
����������1��һ�������������=����ǰ��������1+�����ʣ���2015��ҪͶ�����������2900��1+x����Ԫ����2015��Ļ�����������x������2016��Ľ���������������г�������⣻
��2�����ã�1������õ�����������2018��õ�����Ͷ��������ѣ����⿼����һԪ���η����������ʵ�֪ʶ������ǰ��������1+��ƽ�������ʣ�����=�����������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾ�������У��߶�AB��ֱ��a��ͼ��ʾ������ֽ��ÿ��С�����εı߳���Ϊ1���߶�AB�������˵���ڸ���ϣ�
��1����ͼ�л������߶�ABΪһ�ߵ������� ABCD���ҵ�C�͵�D���ڸ���ϣ�
��ֱ��д�������� ABCD�����Ϊ�� ����
��2����ͼ�����߶�ABΪһ���ĵ���������ABE����E�ڸ���ϣ������������ĵ�E��_____������
��3����ͼ�е�ֱ��a����һ��Q��ʹ�á�QAB���ܳ���С.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����AOB �� ��������A��O��B����ʹ��A��O��B��=��AOB �� ������
����________ΪԲ�ģ�________Ϊ�뾶�������ֱ�OA �� OB�ڵ�C �� D ��
�ڻ�һ������O��A������________ΪԲ�ģ�________��Ϊ�뾶��������O��A���ڵ�C�䣬
���Ե�________ΪԲ��________��Ϊ�뾶���������2���������Ļ����ڵ�D�䣮
�ܹ���________������O��B�������A��O��B��=��AOB ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ������ABC�ı�AB��AC������������ABDE��������ACFG�����ж���ABC����AEG���֮��Ĺ�ϵ����˵�����ɡ�
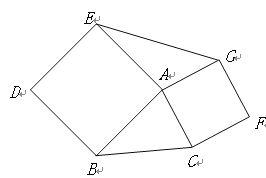
��2����С·������ͨ�ģ���ͼ2��ʾ��С·�ɰ�ɫ����������ʯ�ͺ�ɫ����������ʯ�̳ɣ���֪�м�����������ε����֮����aƽ���ף���Ȧ�����������ε����֮����bƽ���ף�����С·һ��ռ�ض���ƽ���ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������A1B1C1O��A2B2C2C1��A3B3C3C2��������ͼ�ķ�ʽ���ã���C1��C2��C3����x��������A1��A2��A3����ֱ��l����A1��0��1������A2 A1B1=45�㣬���Bn������Ϊ____________����n�Ĵ���ʽ��ʾ��nΪ����������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABCD�У�AB=3��BC=5���Ե�BΪԲ�ģ������ⳤΪ�뾶�������ֱ�BA��BC�ڵ�P��Q���ٷֱ���P��QΪԲ�ģ��Դ��� ![]() PQ�ij�Ϊ�뾶�����������ڡ�ABC�ڽ��ڵ�M������BM���ӳ���AD�ڵ�E����DE�ij�Ϊ
PQ�ij�Ϊ�뾶�����������ڡ�ABC�ڽ��ڵ�M������BM���ӳ���AD�ڵ�E����DE�ij�Ϊ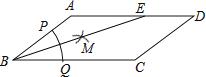
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��a��b����ABC�ǵȱ������Σ���A��ֱ��a�ϣ���BC��ֱ��b�ϣ�����ABC��BC����ƽ��BC��һ��õ���A��B��C������ͼ�٣����������ϵ�ƽ�Ƶõ�ͼ�ڣ��ټ������ϵ�ƽ�Ƶõ�ͼ�������������ڵ�2018��ͼ���еȱ������εĸ�����_________��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com