
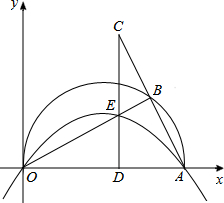
 ��ͼ����ƽ��ֱ������ϵ�У���A��10��0������OAΪֱ���ڵ�һ����������Բ��BΪ��Բ��һ�㣬����AB���ӳ���C��ʹBC=AB����C��CD��x���ڵ�D�����߶�OB�ڵ�E����֪CD=8�������߾���O��E��A���㣮
��ͼ����ƽ��ֱ������ϵ�У���A��10��0������OAΪֱ���ڵ�һ����������Բ��BΪ��Բ��һ�㣬����AB���ӳ���C��ʹBC=AB����C��CD��x���ڵ�D�����߶�OB�ڵ�E����֪CD=8�������߾���O��E��A���㣮���� ��1������Բ�ܽǶ�����ֱ�����Ե�Բ�ܽǵ���90�㣬���ɵó��𰸣�
��2�����ã�1���еĽ�����OB�ǵĴ�ֱƽ���ߣ��õ�B����C�����꣬�ɵ�O����B��������OB����ֱ�ߵĽ���ʽ���Ӷ��ó���E�����꣬�ô���ϵ�����������ߵĽ���ʽ��
��3�����ã�2���Ľ����õ�P�����꣬�������ۢ�����P��CD����࣬�ӳ�OP��CD��Q������ͼ2����OP����ֱ�ߵĺ�����ϵʽ����ʾ��Q��������꣬
��QE�ij�����ʾ���ı���POAE�������������P��CD���Ҳ࣬�ӳ�AP��CD��Q������ͼ3����AP����ֱ�ߵĽ���ʽ���Ӷ����Q��������꣬��QE����ı���POAE���������P��CD�Ҳ�ʱ���ı���POAE��������ֵΪ16����ʱ��P��λ�þ�һ������$-\frac{3}{8}p^2+\frac{9}{4}p+15$=16�����p���ó����ۣ�
���  �⣺��1����OA�ǡ�O��ֱ����
�⣺��1����OA�ǡ�O��ֱ����
���OBA=90�㣬
�ʴ�Ϊ��90��
��2������OC����ͼ1��ʾ��
���ɣ�1��֪OB��AC����AB=BC��
��OB��AC�Ĵ�ֱƽ���ߣ�
��OC=OA=10��
��Rt��OCD��OC=10��CD=8��
��OD=6��
��C��6��8����B��8��4��
��OB����ֱ�ߵĺ�����ϵΪy=$\frac{1}{2}$x��
�֡�E��ĺ�����Ϊ6��
��E��������Ϊ3��
��E��6��3����
�����߹�O��0��0����E��6��3����A��10��0����
����������ߵĺ�����ϵʽΪy=ax��x-10������E���������ã�
3=6a��6-10����
���a=-$\frac{1}{8}$��
��������ߵĺ�����ϵʽΪy=-$\frac{1}{8}$x��x-10������y=-$\frac{1}{8}$x2+$\frac{5}{4}$x��
��3�����P��p��-$\frac{1}{8}$p2+$\frac{5}{4}$p����
������P��CD����࣬�ӳ�OP��CD��Q������ͼ2��
OP����ֱ�ߺ�����ϵʽΪ��y=��-$\frac{1}{8}$p+$\frac{5}{4}$��x
�൱x=6ʱ��y=$-\frac{3}{4}p+\frac{15}{2}$����Q��������Ϊ$-\frac{3}{4}p+\frac{15}{2}$��
��QE=$-\frac{3}{4}p+\frac{15}{2}$-3=$-\frac{3}{4}p+\frac{9}{2}$��
S�ı���POAE
=S��OAE+S��OPE
=S��OAE+S��OQE-S��PQE
=$\frac{1}{2}$•OA•DE+$\frac{1}{2}$QE•OD-$\frac{1}{2}$•QE•Px•
=$\frac{1}{2}$��10��3+$\frac{1}{2}$����-$\frac{3}{4}$p+$\frac{9}{2}$����6-$\frac{1}{2}$•��$-\frac{3}{4}p+\frac{9}{2}$��•��6-p����
=$-\frac{3}{8}p^2+\frac{9}{4}p+15$
������P��CD���Ҳ࣬�ӳ�AP��CD��Q������ͼ3��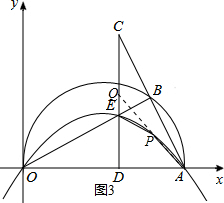
P��p��-$\frac{1}{8}$p2+$\frac{5}{4}$p����A��10��0��
����AP����ֱ�߷���Ϊ��y=kx+b����P��A�������ã�
$\left\{\begin{array}{l}10k+b=0\\ pk+b=-\frac{1}{8}p^2+\frac{5}{4}p\end{array}$��
���$\left\{\begin{array}{l}k=-\frac{1}{8}p\\ b=\frac{5}{4}p\end{array}$��
��AP����ֱ�߷���Ϊ��y=$-\frac{1}{8}p$x+$\frac{5}{4}p$��
�൱x=6ʱ��y=$-\frac{1}{8}p$•6+$\frac{5}{4}p$=$\frac{1}{2}$P����Q��������Ϊ$\frac{1}{2}$P��
��QE=$\frac{1}{2}$P-3��
��S�ı���POAE
=S��OAE+S��APE
=S��OAE+S��AQE-S��PQE
=$\frac{1}{2}$•OA•DE+$\frac{1}{2}$•QE•DA-$\frac{1}{2}$•QE•��Px-6��
=$\frac{1}{2}$��10��3+$\frac{1}{2}$•QE•��DA-Px+6��
=15+$\frac{1}{2}$•��$\frac{1}{2}$p-3��•��10-p��
=$-\frac{1}{4}p^2+4p$
=$-\frac{1}{4}��p-8��^2+16$��
�൱P��CD�Ҳ�ʱ���ı���POAE��������ֵΪ16����ʱ��P��λ�þ�һ����
��$-\frac{3}{8}p^2+\frac{9}{4}p+15$=16����ã�p=3��$\frac{\sqrt{57}}{3}$��
�൱P��CD���ʱ���ı���POAE���������16�Ķ�ӦP��λ����������
������֪����P��O��A��EΪ������ı������S����16ʱ����Ӧ�ĵ�P����ֻ��3����
���� ������Ҫ������Բ�ܽǶ��������κ�����������⣬�����������ؼ������ڽ���������ת��Ϊ�������⣬Ȼ�����ν�Ͻ�����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
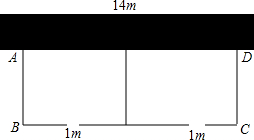 ��ͼ��Ҫ��һ������������������Ϊ��Ƭ������������һ�߿���һ�泤14m��ǽ�����������м�����ı����ܳ�22m������Χ�ɣ�ÿƬ��������ǰ�����һ�ȿ�Ϊ1m���ţ��������������������������ҪΧ�������Ϊ45m2����������������������Ŀ�AB=x�ף���A��D����ľ�����ú�x�ķ�ʽ��ʾΪ$\frac{45}{24-3x}$�����������ܳ�Ϊ22m�����з�ʽ����$\frac{45}{24-3x}$+3x-2=22��x=5���������еķ��̲�����������x=3�أ���˵�����ɣ�
��ͼ��Ҫ��һ������������������Ϊ��Ƭ������������һ�߿���һ�泤14m��ǽ�����������м�����ı����ܳ�22m������Χ�ɣ�ÿƬ��������ǰ�����һ�ȿ�Ϊ1m���ţ��������������������������ҪΧ�������Ϊ45m2����������������������Ŀ�AB=x�ף���A��D����ľ�����ú�x�ķ�ʽ��ʾΪ$\frac{45}{24-3x}$�����������ܳ�Ϊ22m�����з�ʽ����$\frac{45}{24-3x}$+3x-2=22��x=5���������еķ��̲�����������x=3�أ���˵�����ɣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����Rt��ABC�У���ACB=90�㣬AC=8��BC=6��CD��AB������ΪD����tan��BCD��ֵ��$\frac{3}{4}$��
��ͼ����Rt��ABC�У���ACB=90�㣬AC=8��BC=6��CD��AB������ΪD����tan��BCD��ֵ��$\frac{3}{4}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2�� | B�� | 4�� | C�� | 5�� | D�� | 6�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
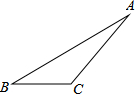 ��ͼ��һ���ABC���ϣ���֪AB=20cm��BC=7cm��AC=15cm���ֽ����ϲü���һ��Բ�β��ϣ����Բ���������ǣ�������
��ͼ��һ���ABC���ϣ���֪AB=20cm��BC=7cm��AC=15cm���ֽ����ϲü���һ��Բ�β��ϣ����Բ���������ǣ�������| A�� | ��cm2 | B�� | 2��cm2 | C�� | 4��cm2 | D�� | 8��cm2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
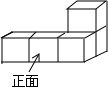 ��ͼ����5����ȫ��ͬ��С��������ɵļ����壮����������������ͼ�ǣ�������
��ͼ����5����ȫ��ͬ��С��������ɵļ����壮����������������ͼ�ǣ�������| A�� | 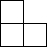 | B�� |  | C�� | 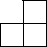 | D�� | 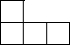 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com