
【题目】如图,在平行四边形ABCD中,过对角线BD的中点O作直线EF,分别交DA的延长线,AB, DC,BC的延长线于点E,M,N,F.
(1)求证:△ODE≌△OBF;
(2)除(1)中这对全等三角形外,再写出两对全等三角形(不需要证明).
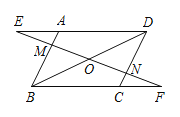
【答案】(1)见解析(2)△AME≌△CNF、△BOM≌△DON
【解析】
(1)根据AAS即可证明△ODE≌△OBF;
(2)根据平时四边形的性质即可写出两对全等三角形.
解:(1)证明:在平行四边形ABCD中,OD=OB,AD∥BC,
∴∠1 =∠2 ,∠E =∠F.
在△ODE和△OBF中,

∴△ODE≌△OBF.

(2)∵四边形ABCD是平行四边形,
∴∠BAD=∠DCB,
∴∠EAM=∠FCN
∵△ODE≌△OBF.
∴AE=ED-AD=BF-BC=CF,
∵DE∥BF,
∴∠E=∠F,
∴△AME≌△CNF(ASA)
∵四边形ABCD是平行四边形,
∴BO=DO,AB∥CD
∴∠MBO=∠NDO,∠BMO=∠DNO
∴△BOM≌△DON.
∴△AME≌△CNF、△BOM≌△DON.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
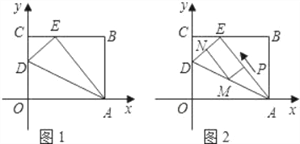
【题目】如图1,OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=5,OC=4.
(1)在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求D,E两点的坐标;
(2)如图2,若AE上有一动点P(不与A,E重合)自A点沿AE方向E点匀速运动,运动的速度为每秒1个单位长度,设运动的时间为t秒(0<t<5),过P点作ED的平行线交AD于点M,过点M作AE平行线交DE于点N.求四边形PMNE的面积S与时间t之间的函数关系式;当t取何值时,s有最大值,最大值是多少?
(3)在(2)的条件下,当t为何值时,以A,M,E为顶点的三角形为等腰三角形,并求出相应的时刻点M的坐标?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,点C在∠AOB的一边OA上,过点C的直线DE∥OB,CF平分∠ACD,CG⊥CF于点C.
(1)若∠O=40°,求∠ECF的度数;
(2)求证:CG平分∠OCD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2与y轴交于点C(0,4),其中x1,x2是方程x2﹣4x﹣12=0的两个根.
(1)求抛物线的解析式;
(2)点M是线段AB上的一个动点,过点M作MN∥BC,交AC于点N,连结CM,当△CMN的面积最大时,求点M的坐标;
(3)点D(4,k)在(1)中抛物线上,点E为抛物线上一动点,在x轴上是否存在点F,使以A、D、E、F为顶点的四边形是平行四边形?如果存在,直接写出所有满足条件的点F的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
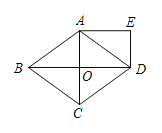
【题目】如图,菱形ABCD的对角线AC,BD相交于点O,且DE∥AC,AE∥BD.
(1)求证:四边形AODE是矩形.
(2)若AB=5,BD=8,求矩形AODE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]()
![]() 在第一象限内的图像交于
在第一象限内的图像交于![]() 和
和![]() 两点.
两点.

(1)求反比例函数的表达式;
(2)在第一象限内,当一次函数![]() 的值大于反比例函数
的值大于反比例函数![]()
![]() 的值时,写出自变量
的值时,写出自变量![]() 的取值范围;
的取值范围;
(3)求![]() 面积.
面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
= y2+8y+16 (第二步)
=(y+4)2 (第三步)
=(x2-4x+4)2 (第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 B.平方差公式 C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)
若不彻底,请直接写出因式分解的最后结果_________.
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com