
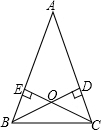
 如图,在△ABC中,AB=AC,BD、CE是腰AB、AC上的高,交于点O.
如图,在△ABC中,AB=AC,BD、CE是腰AB、AC上的高,交于点O.分析 (1)首先根据等腰三角形的性质得到∠ABC=∠ACB,然后利用高线的定义得到∠ECB=∠DBC,从而得证;
(2)首先求出∠A的度数,进而求出∠COD的度数.
解答 (1)证明:∵AB=AC,
∴∠ABC=∠ACB,
∵BD、CE是△ABC的两条高线,
∴∠BEC=∠BDC=90°,
在△BEC和△CDB中,
$\left\{\begin{array}{l}{∠BEC=∠CDB}\\{∠EBC=∠DCB}\\{BC=CB}\end{array}\right.$,
∴△BEC≌△CDB,
∴∠DBC=∠ECB,BE=CD,
在△BOE和△COD中,
$\left\{\begin{array}{l}{∠BOE=∠COD}\\{BE=CD}\\{∠BEC=∠BDE}\end{array}\right.$,
∴△BOE≌△COD,
∴OB=OC;
(2)解:∵∠ABC=65°,AB=AC,
∴∠A=180°-2×65°=50°,
∴∠COD=∠A=50°.
点评 本题考查了等腰三角形的性质及三角形的内角和定理;关键是掌握等腰三角形等角对等边.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,小明的家D距离大树底部A是9米,一次台风过后,大树在离地面3米的点B处折断,顶端着地处点C在AD上,又知BC恰好等于CD.
如图,小明的家D距离大树底部A是9米,一次台风过后,大树在离地面3米的点B处折断,顶端着地处点C在AD上,又知BC恰好等于CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
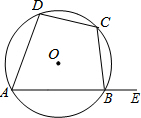 如图,四边形ABCD的四个顶点都在⊙O上,∠ADC=85°,在探究“四点共圆的条件”的活动中,知道∠ADC与∠ABC互补,若∠EBC是ABCD的一个外角,则∠EBC=85°.
如图,四边形ABCD的四个顶点都在⊙O上,∠ADC=85°,在探究“四点共圆的条件”的活动中,知道∠ADC与∠ABC互补,若∠EBC是ABCD的一个外角,则∠EBC=85°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
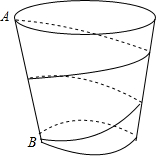 如图,一只杯子的上下底面分别是直径为5cm和7.5cm的圆,母线AB的长为15cm.
如图,一只杯子的上下底面分别是直径为5cm和7.5cm的圆,母线AB的长为15cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
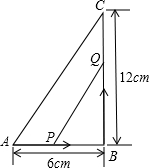 如图,在△ABC中,∠B=90°,点P从点A开始,沿AB向点B以1cm/s的速度移动,点Q从B点开始沿BC 以2cm/s的速度移动,如果P、Q分别从A、B同时出发:
如图,在△ABC中,∠B=90°,点P从点A开始,沿AB向点B以1cm/s的速度移动,点Q从B点开始沿BC 以2cm/s的速度移动,如果P、Q分别从A、B同时出发:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com