练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】计算：

    （1）2﹣（﹣4）+3

    （2）﹣32÷（﹣2）3

    （3）（﹣+）×12

    （4）﹣13+[（﹣4）2﹣（1﹣32）×2]

    【答案】（1）9；（2）4；（3）7；（4）31

    【解析】

    （1）先化简，再计算加减法即可求解；

    （2）先算乘方，再算乘除，最后算加减；同级运算，应按从左到右的顺序进行计算；如果有括号，要先做括号内的运算；

    （3）根据乘法分配律简便计算；

    （4）先算乘方，再算乘除，最后算加减；同级运算，应按从左到右的顺序进行计算；如果有括号，要先做括号内的运算.

    （1）2﹣（﹣4）+3＝2+4+3＝9；

    （2）﹣32÷（﹣2）3＝﹣32÷（﹣8）＝4；

    （3）（﹣+）×12＝×12﹣×12+×12＝6﹣8+9＝7；

    （4）﹣13+[（﹣4）2﹣（1﹣32）×2]

    ＝﹣1+[16﹣（1﹣9）×2]

    ＝﹣1+（16+8×2）

    ＝﹣1+（16+16）

    ＝﹣1+32

    ＝31．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】请阅读下列材料，并完成相应的任务。
    阿基米德(Archimedes,公元前287~公元前212年,古希腊)是有史以来最伟大的数学家之一.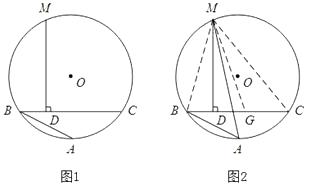

    阿基米德折弦定理：如图1，AB和BC是圆O的两条弦（即折线ABC是圆的一条折弦）， BC＞AB，M是 的中点，即CD=AB+BD。下面是运用“截长法”证明CD=AB+BD的部分过程。
    证明：如图2，在CB上截取CG=AB，连接MA、MB、MC、MG。因为M是弧ABC的中点，所以MA=MC.
    任务：
    （1）请按照上面的证明思路，完整证明阿基米德折弦定理，即CD=AB+BD。
    （2）如图3，已知等边△ABC内接于圆O，AB=1，D为 上一点，∠ABD=45°，AE⊥BD于点E，则△BDC的周长是.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】仔细阅读下面的例题：

    例题：已知二次三项式x2－4x＋m有一个因式是x＋3，求另一个因式以及m的值．

    解：设另一个因式为x＋n，则

    x2－4x＋m＝(x＋3)(x＋n)，

    ∴x2－4x＋m＝x2＋(n＋3)x＋3n，

    ∴，解得，

    ∴另一个因式为x－7，m的值为－21.

    问题：仿照以上方法解答下面的问题：

    已知二次三项式2x2＋3x－k有一个因式是2x－5，求另一个因式以及k的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知抛物线y=﹣ x2﹣ x+2与x轴交于A、B两点，与y轴交于点C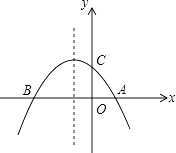

    （1）求点A，B，C的坐标；
    （2）点E是此抛物线上的点，点F是其对称轴上的点，求以A，B，E，F为顶点的平行四边形的面积；
    （3）此抛物线的对称轴上是否存在点M，使得△ACM是等腰三角形？若存在，请求出点M的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了庆祝即将到来的2018年国庆节，某校举行了书法比赛，赛后整理了参赛同学的成绩，并制作了如下两幅不完整的统计图表

    分数段

    频数

    频率

    60≤x＜70

    30

    0.15

    70≤x＜80

    m

    0.45

    80≤x＜90

    60

    n

    90≤x＜100

    20

    0.1

    请根据以上图表提供的信息，解答下列问题：

    （1）这次共调查了　 　名学生；表中的数m=　 　，n=　 　．

    （2）请补全频数直方图；

    （3）若绘制扇形统计图，则分数段60≤x＜70所对应的扇形的圆心角的度数是　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

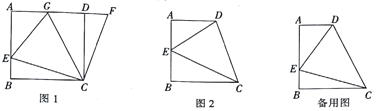
    【题目】如图1，在正方形ABCD中，点E是AB上一点，点F是AD延长线上一点，且DF=BE，连接CE、CF．

    （1）求证：CE=CF．

    （2）在图1中，若点G在AD上，且∠GCE=45°，则GE=BE+GD成立吗？为什么？

    （3）根据你所学的知识，运用（1）、（2）解答中积累的经验，完成下列各题，如图2，在四边形ABCD中，AD∥BC（BC＞AD），∠B=90°，AB=BC，且∠DCE=45°．

    ①若AE=6，DE=10，求AB的长；

    ②若AB=BC=9，BE=3，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ACB=90°，点D，E分别是边BC，AB上的中点，连接DE并延长至点F，使EF=2DF，连接CE、AF．

    （1）证明：AF=CE；

    （2）当∠B=30°时，试判断四边形ACEF的形状并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，正方形ABCD与正方形AEFG起始时互相重合，现将正方形AEFG绕点A逆时针旋转，设旋转角∠BAE=α（0°＜α＜360°），则当正方形的顶点F落在正方形的对角线AC或BD所在直线上时，α= ．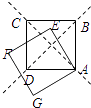

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，四边形ABCD是菱形，对角线AC=8 cm，BD=6cm，DH⊥AB于H，求DH的长．

    查看答案和解析>>

    同步练习册答案