
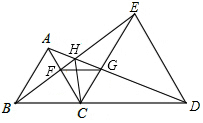
 已知,点C是线段BD上一动点,分别以BC、CD为边向同侧作等边△ABC和等边三角形△CDE,如图所示.
已知,点C是线段BD上一动点,分别以BC、CD为边向同侧作等边△ABC和等边三角形△CDE,如图所示.分析 (1)可以根据SAS即可证明;
(2)∠AHB的大小不变.利用“8字型”证明∠AHF=∠FCB=60°即可;
(3)由△BCF≌△ACG,推出CF=CG,由∠FCG=60°,推出△FCG是等边三角形,推出∠FGC=∠GCD=60°,即可推出FG∥BD;
解答 (1)证明:∵△ABC,△CDE都是等边三角形,
∴BC=CA,CE=CD,∠ACB=∠ECD=60°,
∴∠BCE=△ACB,
在△BCE和△ACD中,
$\left\{\begin{array}{l}{CB=CA}\\{∠BCE=∠ACD}\\{CE=CD}\end{array}\right.$,
∴△BCE≌△ACD.
(2)解:∠AHB的大小不变.
理由:∵△BCE≌△ACD,
∴∠CBF=∠FAH,
∵∠AFH=∠BFC,
∴∠AHF=∠ACB=60°,
即∠AHB=60°.
(3)解:结论:FG∥BD.
理由:在△BCF和△ACG中,
$\left\{\begin{array}{l}{∠CBF=∠CAG}\\{BC=CA}\\{∠BCF=∠ACG=60°}\end{array}\right.$,
∴△BCF≌△ACG,
∴CF=CG,
∵∠FCG=60°,
∴△FCG是等边三角形,
∴∠FGC=∠GCD=60°,
∴FG∥BD.
点评 本题考查全等三角形的判定和性质、等边三角形的性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学为了响应国家发展足球的战略方针,激发学生对足球的兴趣,特举办全员参与的“足球比赛”,赛后,全校随机抽查部分学生,其成绩(百分制)整理分成5组,并制成如下频数分布表和扇形统计图,请根据所提供的信息解答下列问题:
某中学为了响应国家发展足球的战略方针,激发学生对足球的兴趣,特举办全员参与的“足球比赛”,赛后,全校随机抽查部分学生,其成绩(百分制)整理分成5组,并制成如下频数分布表和扇形统计图,请根据所提供的信息解答下列问题:| 组别 | 成绩(分) | 频数 |
| A | 50≤x<60 | 6 |
| B | 60≤x<70 | m |
| C | 70≤x<80 | 20 |
| D | 80≤x<90 | 36 |
| E | 90≤x<100 | n |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
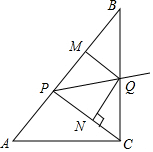 如图,已知:在Rt△ABC中,斜边AB=10,sinA=$\frac{4}{5}$,点P为边AB上一动点(不与A,B重合),PQ平分∠CPB交边BC于点Q,QM⊥AB于M,QN⊥CP于N.
如图,已知:在Rt△ABC中,斜边AB=10,sinA=$\frac{4}{5}$,点P为边AB上一动点(不与A,B重合),PQ平分∠CPB交边BC于点Q,QM⊥AB于M,QN⊥CP于N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com