
【题目】在学习了矩形后,数学活动小组开展了探究活动.如图1,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在
在![]() 上,先以
上,先以![]() 为折痕将
为折痕将![]() 点往右折,如图2所示,再过点
点往右折,如图2所示,再过点![]() 作
作![]() ,垂足为
,垂足为![]() ,如图3所示.
,如图3所示.
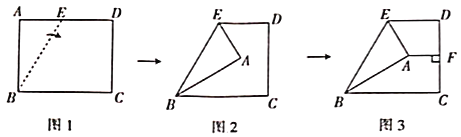
(1)在图3中,若![]() ,则
,则![]() 的度数为______,
的度数为______,![]() 的长度为______.
的长度为______.
(2)在(1)的条件下,求![]() 的长.
的长.
(3)在图3中,若![]() ,则
,则![]() ______.
______.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】将三角形纸片△ABC按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF.已知AB=AC=8,BC=10,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 、
、![]() 在
在![]() 上,点
上,点![]() 在
在![]() 外,边
外,边![]() 、
、![]() 与
与![]() 交于点
交于点![]() 、
、![]() ,
,![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
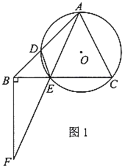
(1)求证:![]() ;
;
(2)当![]() 时,求
时,求![]() 的长;
的长;
(3)设![]() ,
,![]() 的面积为
的面积为![]() ,
,
①求![]() 关于
关于![]() 的函数关系式.
的函数关系式.
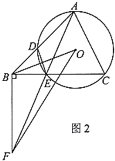
②如图2,连接![]() 、
、![]() ,若
,若![]() 的面积是
的面积是![]() 的面积的1.5倍时,求
的面积的1.5倍时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从甲地到乙地有A,B,C三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
线路 公交车用时的频数 公交车用时 | 30<t ≤35 | 35<t ≤40 | 40<t ≤45 | 45<t ≤50 | 合计 |
A | 59 | 151 | a | 124 | 500 |
B | 50 | b | 122 | 278 | 500 |
C | 45 | 265 | 167 | c | 500 |
(1)将上面表格补充完整;
(2)某天王先生和李女士从甲地到乙地,试用树状图或列表法求在早高峰期间两人刚好乘坐同一条线路的概率;
(3)小张从甲地到乙地,早高峰期间用时不超过45分钟,请问小张应该选择哪条线路?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在△ABC中,∠BAC=90°,AB=AC.
(1)如图1,将线段AC绕点A逆时针旋转60°得到AD,连结CD、BD,∠BAC的平分线交BD于点E,连结CE.
①求证:∠AED=∠CED;
②用等式表示线段AE、CE、BD之间的数量关系(直接写出结果);
(2)在图2中,若将线段AC绕点A顺时针旋转60°得到AD,连结CD、BD,∠BAC的平分线交BD的延长线于点E,连结CE.请补全图形,并用等式表示线段AE、CE、BD之间的数量关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y关于x的函数表达式是![]() ,下列结论不正确的是( )
,下列结论不正确的是( )
A.若![]() ,函数的最大值是5
,函数的最大值是5
B.若![]() ,当
,当![]() 时,y随x的增大而增大
时,y随x的增大而增大
C.无论a为何值时,函数图象一定经过点![]()
D.无论a为何值时,函数图象与x轴都有两个交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是由五个完全相同的小正方体组成的立体图形,将图①中的一个小正方体改变位置后如图②.则三视图发生改变的是( )
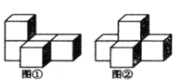
A.主视图B.俯视图
C.左视图D.主视图、俯视图和左视图
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com