
【题目】如图,已知矩形![]() ,对角线
,对角线![]() 的垂直平分线分别交
的垂直平分线分别交![]() ,
,![]() 和
和![]() 于点
于点![]() ,
,![]() ,
,![]() .
.![]() ,
,![]() 的延长线交于点
的延长线交于点![]() ,且
,且![]() ,连接
,连接![]() .
.
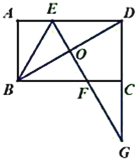
(1)求证:![]()
(2)求证:![]() 平分
平分![]() .
.
【答案】(1)见解析;(2)见解析.
【解析】
(1)垂直平分线的定义可得∠EOD=90°,根据矩形的性质可得∠FCG=90°,AD//BC,根据平行线的性质可得∠DEO=∠CFG,利用AAS即可证明△DOE≌△GCF;
(2)根据全等三角形的性质可得OE=CF,利用AAS可证明![]() ,可得DE=BF,根据线段的和差关系可得AE=CF,即可得出AE=OE,根据到角两边距离相等的点在角的角平分线上即可得出BE平分∠ABD.
,可得DE=BF,根据线段的和差关系可得AE=CF,即可得出AE=OE,根据到角两边距离相等的点在角的角平分线上即可得出BE平分∠ABD.
(1)∵![]() 是
是![]() 垂直平分线,
垂直平分线,
∴![]() ,
,
∵四边形![]() 是矩形,
是矩形,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
在△DOE和△GCF中,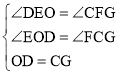 ,
,
∴△DOE≌△GCF.
(2)由(1)![]() 可得:
可得:
![]() ,
,
∵![]() 是
是![]() 垂直平分线,
垂直平分线,
∴![]() ,
,
在△EOD和△FOB中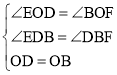 ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴AD-DE=BC-BF,即AE=CF,
∴AE=OE,
∵∠A=∠BOE=90°,
∴![]() 平分
平分![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,tan∠A=![]() ,M,N分别在AD,BC上,将四边形AMNB沿MN翻折,使AB的对应线段EF经过顶点D,当EF⊥AD时,
,M,N分别在AD,BC上,将四边形AMNB沿MN翻折,使AB的对应线段EF经过顶点D,当EF⊥AD时,![]() 的值为_____.
的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
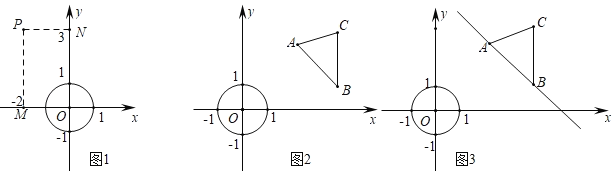
【题目】在平面直角坐标系xOy,对于点P(xp,yp)和图形G,设Q(xQ,yQ)是图形G上任意一点,|xp﹣xQ|的最小值叫点P和图形G的“水平距离”,|yp﹣yQ|的最小值叫点P和图形G的“竖直距离”,点P和图形G的“水平距离”与“竖直距离”的最大值叫做点P和图形G的“绝对距离”
例如:点P(﹣2,3)和半径为1的⊙O,因为⊙O上任一点Q(xQ,yQ)满足﹣1≤xQ≤1,﹣1≤yQ≤1,点P和⊙O的“水平距离”为|﹣2﹣xQ|的最小值,即|﹣2﹣(﹣1)|=1,点P和⊙O的“竖直距离”为|3﹣yQ|的最小值即|3﹣1|=2,因为2>1,所以点P和⊙O的“绝对距离”为2.
已知⊙O半径为1,A(2,![]() ),B(4,1),C(4,3)
),B(4,1),C(4,3)
(1)①直接写出点A和⊙O的“绝对距离”
②已知D是△ABC边上一个动点,当点D与⊙O的“绝对距离”为2时,写出一个满足条件的点D的坐标;
(2)已知E是△ABC边一个动点,直接写出点E与⊙O的“绝对距离”的最小值及相应的点E的坐标
(3)已知P是⊙O上一个动点,△ABC沿直线AB平移过程中,直接写出点P与△ABC的“绝对距离”的最小值及相应的点P和点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读:设试验结果落在某个区域S中每一点的机会均等,用A表示事件“试验结果落在S中的一个小区域M中”,那么事件A发生的概率P(A)![]() .在桌面上放一张50 cm×50 cm的正方形白纸ABCD,⊙O是它的内切圆,小明随机地将1000粒大米撒到该白纸上,其中落在圆内的大米有800粒,由此可得圆周率
.在桌面上放一张50 cm×50 cm的正方形白纸ABCD,⊙O是它的内切圆,小明随机地将1000粒大米撒到该白纸上,其中落在圆内的大米有800粒,由此可得圆周率![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数![]() ,一次函数
,一次函数![]() ,若方程
,若方程![]() 的两根是
的两根是![]() ,
,![]() .
.
(1)求b、c的值;
(2)当x满足![]() 时,比较
时,比较![]() 与x的大小并说明理由;
与x的大小并说明理由;
(3)设点M的坐标是![]() ,点P是抛物线
,点P是抛物线![]() 上的一个动点,当点P到点M的距离与到直线
上的一个动点,当点P到点M的距离与到直线![]() 的距离之和最小时,请直接写出点P坐标.
的距离之和最小时,请直接写出点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了解七年级学生喜欢球类活动的情况,采取抽样调查的方法,从足球、乒乓球、篮球、排球等四个方面随机调查了部分七年级学生的兴趣爱好,根据调查的结果组建了![]() 个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:
个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:
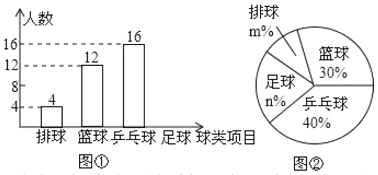
(1)求被抽查学生人数,将条形统计图补充完整;
(2)求出扇形统计图中,排球部分对应的圆心角度数;
(3)如果该中学七年级共有![]() 名学生,请你估计七年级学生中喜欢排球的学生有多少名?
名学生,请你估计七年级学生中喜欢排球的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为更好开展“课后延时”服务,某校抽取了部分七年级学生,就课后活动项目进行调查.学校根据学生前期统计给出了如下四个选项:![]() “球类”、
“球类”、![]() “棋类”、
“棋类”、![]() “计算机信息类”、
“计算机信息类”、![]() “其他”,并将最终调查结果绘制成如下两幅不完整的统计图.
“其他”,并将最终调查结果绘制成如下两幅不完整的统计图.

根据图中提供的信息,解决下列问题:
(1)本次调查共抽取了____名学生,扇形统计图中,![]() 类所对应的扇形圆心角大小为
类所对应的扇形圆心角大小为
(2)将条形统计图补充完整;
(3)已知选择![]() 类的同学有两位来自七(1)班,其余来自七(2)班,调查组准备从选
类的同学有两位来自七(1)班,其余来自七(2)班,调查组准备从选![]() 类同学中任选两位做细致分析求两位同学来自同一个班级的概率.
类同学中任选两位做细致分析求两位同学来自同一个班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
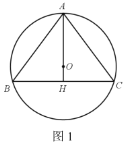
【题目】如图1,已知,⊙O是△ABC的外接圆,AB=AC=10,BC=12,连接AO并延长交BC于点H.
(1)求外接圆⊙O的半径;
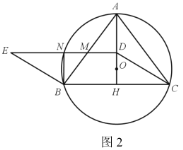
(2)如图2,点D是AH上(不与点A,H重合)的动点,以CD,CB为边,作平行四边形CDEB,DE分别交⊙O于点N,交AB边于点M.
①连接BN,当BN⊥DE时,求AM的值;
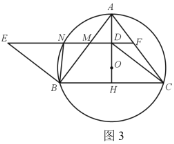
②如图3,延长ED交AC于点F,求证:NM·NF=AM·MB;
③设AM=x,要使![]() -2
-2![]() <0成立,求x的取值范围.
<0成立,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和⊙M(半径为r),给出如下定义:若点P关于点M的对称点为Q,且r≤PQ≤3r,则称点P为⊙M的称心点.
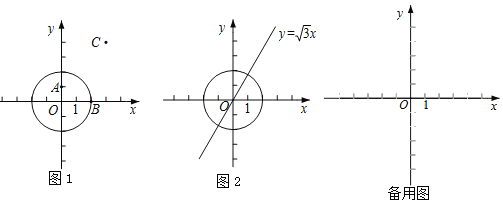
(1)当⊙O的半径为2时,
①如图1,在点A(0,1),B(2,0),C(3,4)中,⊙O的称心点是 ;
②如图2,点D在直线y![]() x上,若点D是⊙O的称心点,求点D的横坐标m的取值范围;
x上,若点D是⊙O的称心点,求点D的横坐标m的取值范围;
(2)⊙T的圆心为T(0,t),半径为2,直线y![]() x+1与x轴,y轴分别交于点E,F.若线段EF上的所有点都是⊙T的称心点,直接写出t的取值范围.
x+1与x轴,y轴分别交于点E,F.若线段EF上的所有点都是⊙T的称心点,直接写出t的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com