
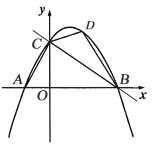
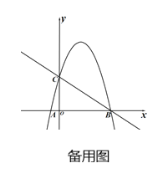
【题目】如图,在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴相交于点B、C,经过点B、C的抛物线
轴相交于点B、C,经过点B、C的抛物线![]() 与
与![]() 轴的另一个交点为A.
轴的另一个交点为A.
(1)求出抛物线表达式,并求出点A坐标;
(2)已知点D在抛物线上,且横坐标为3,求出△BCD的面积;
(3)点P是直线BC上方的抛物线上一动点,过点P作PQ垂直于![]() 轴,垂足为Q.是否存在点P,使得以点A、P、Q为顶点的三角形与△BOC相似?若存在,请求出点P的坐标;若不存在,请说明理由.
轴,垂足为Q.是否存在点P,使得以点A、P、Q为顶点的三角形与△BOC相似?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】(1)y=-![]() x2+
x2+![]() x+4,A(-1,0);(2)18;(3)P(5,4)或P(
x+4,A(-1,0);(2)18;(3)P(5,4)或P(![]() ,
,![]() )时,点A、P、Q为顶点的三角形与△BOC相似.
)时,点A、P、Q为顶点的三角形与△BOC相似.
【解析】
(1)求出B(6,0),C(0,4)并代入y=-![]() x2+bx+c,即可求出解析式;
x2+bx+c,即可求出解析式;
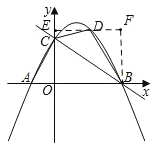
(2)求出D(3,8),过点D作y轴的垂线交于点E,过点B作BF⊥DE交ED的延长线于点F;则E(0,8),F(6,8),所以S△BCD=S梯形ECBF-S△CDE-S△BFD=![]() (EC+BF)×OB-
(EC+BF)×OB-![]() ×EC×ED-
×EC×ED-![]() ×DF×BF,再由所求点确定各边长即可求面积;
×DF×BF,再由所求点确定各边长即可求面积;
(3)点A、P、Q为顶点的三角形与△BOC相似有两种情况:①△PAQ∽△CBO时,由![]() ,则
,则![]() ,求出m;②△PAQ∽△BCO时,
,求出m;②△PAQ∽△BCO时,![]() ,则有
,则有![]() ,求出m.
,求出m.
(1)由已知可求B(6,0),C(0,4),
将点B(6,0),C(0,4)代入y=-![]() x2+bx+c,
x2+bx+c,
则有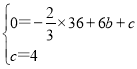 ,
,
解得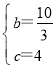 ,
,
∴y=-![]() x2+
x2+![]() x+4,
x+4,
令y=0,则-![]() x2+
x2+![]() x+4=0,
x+4=0,
解得x=-1或x=6,
∴A(-1,0);
(2)∵点D在抛物线上,且横坐标为3,
∴D(3,8),
过点D作y轴的垂线交于点E,过点B作BF⊥DE交ED的延长线于点F;
∴E(0,8),F(6,8),
∴S△BCD=S梯形ECBF-S△CDE-S△BFD=![]() (EC+BF)×OB-
(EC+BF)×OB-![]() ×EC×ED-
×EC×ED-![]() ×DF×BF
×DF×BF
=![]() ×(4+8)×6-
×(4+8)×6-![]() ×4×3-
×4×3-![]() ×3×8
×3×8
=36-6-12
=18;
(3)设P(m,-![]() m2+
m2+![]() m+4),
m+4),
∵PQ垂直于x轴,
∴Q(m,0),且∠PQO=90°,
∵∠COB=90°,
∴点A、P、Q为顶点的三角形与△BOC相似有两种情况:
①△PAQ∽△CBO时,![]() ,
,
∴![]() ,
,
解得m=5或m=-1,
∵点P是直线BC上方的抛物线上,
∴0≤m≤6,
∴m=5,
∴P(5,4);
②△PAQ∽△BCO时,![]() ,
,
∴![]() ,
,
解得m=-1或m=![]() ,
,
∵点P是直线BC上方的抛物线上,
∴0≤m≤6,
∴m=![]() ,
,
∴P(![]() ,
,![]() );
);
综上所述:P(5,4)或P(![]() ,
,![]() )时,点A、P、Q为顶点的三角形与△BOC相似.
)时,点A、P、Q为顶点的三角形与△BOC相似.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在推进郑州市城乡生活垃圾分类的行动中,某社区对居民掌握垃圾分类知识的情况进行调査.其中![]() ,
,![]() 两小区分别有1000名居民参加了测试,社区从中各随机抽取50名居民成绩进行整理得到部分信息:
两小区分别有1000名居民参加了测试,社区从中各随机抽取50名居民成绩进行整理得到部分信息:
(信息一)![]() 小区50名居民成绩的频数直方图如下(每一组含前一个边界值,不含后一个边界值).
小区50名居民成绩的频数直方图如下(每一组含前一个边界值,不含后一个边界值).
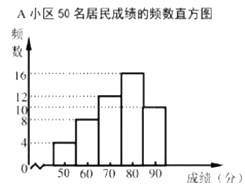
(信息二)上图中,从左往右第四组的成绩如下:
75 | 75 | 79 | 79 | 79 | 79 | 80 | 80 |
81 | 82 | 82 | 83 | 83 | 84 | 84 | 84 |
(信息三)![]() ,
,![]() 两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
两小区各50名居民成绩的平均数、中位数、众数、优秀率(80分及以上为优秀)、方差等数据如下(部分空缺):
小区 | 平均数 | 中位数 | 众数 | 优秀率 | 方差 |
| 75.1 | 79 | 40% | 277 | |
| 75.1 | 77 | 76 | 45% | 211 |
根据以上信息,回答下列问题:
(1)求![]() 小区50名居民成绩的中位数.
小区50名居民成绩的中位数.
(2)请估计![]() 小区1000名居民成绩能超过平均数的人数.
小区1000名居民成绩能超过平均数的人数.
(3)请尽量从多个角度(至少三个),选择合适的统计量分析![]() ,
,![]() 两小区参加测试的居民掌握垃圾分类知识的情况.
两小区参加测试的居民掌握垃圾分类知识的情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知第一象限内的点
中,已知第一象限内的点![]() 在反比例函数y=
在反比例函数y=![]() 的图象上,第二象限内的点B在反比例函数y=
的图象上,第二象限内的点B在反比例函数y=![]() 的图象上,连接
的图象上,连接![]() 、
、![]() ,若
,若![]() ,
,![]() ,则
,则![]() __________.
__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
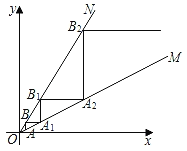
【题目】在平面直角坐标系中,点A(![]() ,1)在射线OM上,点B(
,1)在射线OM上,点B(![]() ,2)在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,则点B1的纵坐标为_____,然后以A1B1为直角边作第三个Rt△A1B1A2,…,依次规律,得到Rt△B2019A2020B2020,则点B2020的纵坐标为_____.
,2)在射线ON上,以AB为直角边作Rt△ABA1,以BA1为直角边作第二个Rt△BA1B1,则点B1的纵坐标为_____,然后以A1B1为直角边作第三个Rt△A1B1A2,…,依次规律,得到Rt△B2019A2020B2020,则点B2020的纵坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,![]() ,AC=3,BC=4.点O为边AB上一点(不与A重合)⊙O是以点O为圆心,AO为半径的圆.当⊙O与三角形边的交点个数为3时,则OA的范围( )
,AC=3,BC=4.点O为边AB上一点(不与A重合)⊙O是以点O为圆心,AO为半径的圆.当⊙O与三角形边的交点个数为3时,则OA的范围( )
A.![]() 或
或![]() B.
B.![]() 或
或![]()
C.![]() D.
D.![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情之下,中华儿女共抗时艰.重庆和湖北同饮长江水,为更好地驰援武汉,打赢防疫攻坚战,我市某公益组织收集社会捐献物资.甲、乙两人先后从![]() 地沿相同路线出发徒步前往
地沿相同路线出发徒步前往![]() 地进行物资捐献,甲出发1分钟后乙再出发,一段时间后乙追上甲,这时甲发现有东西落在
地进行物资捐献,甲出发1分钟后乙再出发,一段时间后乙追上甲,这时甲发现有东西落在![]() 地,于是原路原速返回
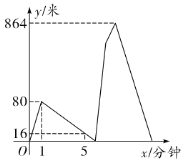
地,于是原路原速返回![]() 地去取(甲取东西的时间忽略不计),而乙继续前行,甲乙两人到达B地后原地帮忙.已知在整个过程中,甲乙均保持各自的速度匀速行走,甲、乙两人相距的路程
地去取(甲取东西的时间忽略不计),而乙继续前行,甲乙两人到达B地后原地帮忙.已知在整个过程中,甲乙均保持各自的速度匀速行走,甲、乙两人相距的路程![]() (米)与甲出发的时间
(米)与甲出发的时间![]() (分钟)之间的函数关系如图所示,则当乙到达
(分钟)之间的函数关系如图所示,则当乙到达![]() 地时,甲距
地时,甲距![]() 地的路程是_______米.
地的路程是_______米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是反比例函数
是反比例函数![]() 的图象上的一点,过点
的图象上的一点,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() .点
.点![]() 为
为![]() 轴正半轴上的一点,连接
轴正半轴上的一点,连接![]() 、
、![]() ,延长
,延长![]() 交
交![]() 轴于点
轴于点![]() .若
.若![]() ,且
,且![]() 的面积为18,则
的面积为18,则![]() 的值是( )
的值是( )
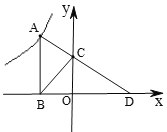
A.6B.-6C.12D.-12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,并回答问题:
定义:平面内与一个定点F和一条定直线l(l不经过点F)距离相等的所有点组成的图形叫抛物线.点F叫做抛物线的焦点,直线l叫做抛物线的准线.
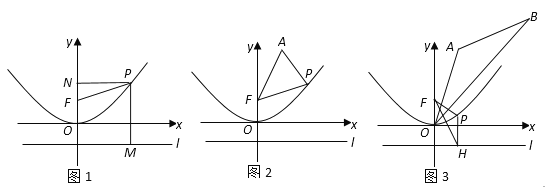
应用:(1)如图1,一条抛物线的焦点为F(0,1),准线为过点(0,-1)且平行于x轴的直线l;设点P(x,y)为抛物线上任意一点,小聪同学在应用定义求这条抛物线的解析式时作出了如下不完整的解答,请你将余下部分补充出来.
解:设点P(x,y)为抛物线上任意一点,作PM⊥l于点M,则PM=_________
作PN⊥y轴于点N,则在△PFN中,有PN=![]() ,NF=
,NF=![]() ,所以PF=__________
,所以PF=__________
∵PF=PM
∴_________=____________,
将方程两边同时平方,解得抛物线的解析式为_____________
(2)如图2,在(1)的条件下,点A(1,3)是坐标平面内一点,则△FAP的周长最小值为________
(3)在(1)(2)的条件下,如图3,点B(4,4)是坐标平面内另一点,过P作PH⊥l,垂足为H,连接PF和FH,问在抛物线上是否存在点P,使得以P,F,H为顶点的三角形与△ABO相似?若存在,求出P点的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com