
【题目】已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题. 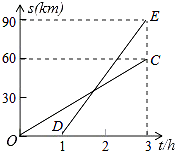
(1)A比B后出发几个小时?B的速度是多少?
(2)在B出发后几小时,两人相遇?
 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】如图,小明家的住房平面图呈长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形的标号为( )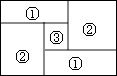
A.①②
B.②③
C.①③
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形纸片ABCD中,AB=BC,AD=CD,∠A=∠C=90°,∠B=150°.将纸片先沿直线BD对折,再将对折后的图形沿从一个顶点出发的直线裁剪,剪开后的图形打开铺平.若铺平后的图形中有一个是面积为2的平行四边形,则CD= . 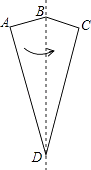
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个古代车轮的碎片,小明为求其外圆半径,连结外圆上的两点A、B,并使AB与车轮内圆相切于点D,做CD⊥AB交外圆于点C.测得CD=10cm,AB=60cm,则这个车轮的外圆半径为cm. 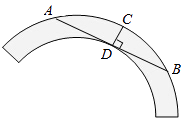
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把球放在长方体纸盒内,球的一部分露出盒外,其主视图如图.⊙O与矩形ABCD的边BC,AD分别相切和相交(E,F是交点),已知EF=CD=8,则⊙O的半径为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 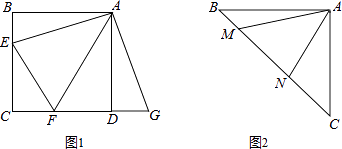
(1)如图1,正方形ABCD中,点E,F分别在边BC,CD上,∠EAF=45°,延长CD到点G,使DG=BE,连结EF,AG.求证:EF=FG.
(2)如图,等腰直角三角形ABC中,∠BAC=90°,AB=AC,点M,N在边BC上,且∠MAN=45°,若BM=1,CN=3,求MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了保护环境,某开发区综合治理指挥部决定购买A,B两种型号的污水处理设备共10台.已知用90万元购买A型号的污水处理设备的台数与用75万元购买B型号的污水处理设备的台数相同,每台设备价格及月处理污水量如下表所示:
污水处理设备 | A型 | B型 |
价格(万元/台) | m | m﹣3 |
月处理污水量(吨/台) | 220 | 180 |
(1)求m的值;
(2)由于受资金限制,指挥部用于购买污水处理设备的资金不超过165万元,问有多少种购买方案?并求出每月最多处理污水量的吨数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,CD⊥AB于点D,⊙D经过点B,与BC交于点E,与AB交与点F.已知tanA= ![]() ,cot∠ABC=
,cot∠ABC= ![]() ,AD=8.
,AD=8. 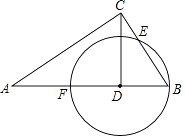
(1)⊙D的半径;
(2)CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加快我省城乡公路建设,我省计划“十三五”期间高速公路运营里程达1000公里,进一步打造城乡快速连接通道,某地计划修建一条高速公路,需在小山东西两侧A,B之间开通一条隧道,工程技术人员乘坐热气球对小山两侧A、B之间的距离进行了测量,他们从A处乘坐热气球出发,由于受西风的影响,热气球以30米/分的速度沿与地面成75°角的方向飞行,25分钟后到达C处,此时热气球上的人测得小山西侧B点的俯角为30°,则小山东西两侧A、B两点间的距离为多少米?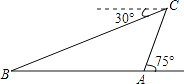
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com