
”¾ĢāÄæ”æĪŖĮĖ¹ÄĄųŹŠĆń½ŚŌ¼ÓĆĖ®£¬ĶņÖŻŹŠ¾ÓĆńÉś»īÓĆĖ®°“½×ĢŻŹ½Ė®¼Ū¼Ę·Ń£¬±ķŹĒøĆŹŠ¾ÓĆń”°Ņ»»§Ņ»±ķ”±Éś»īÓĆĖ®½×ĢŻŹ½¼Ę·Ń¼Ūøń±ķµÄŅ»²æ·ÖŠÅĻ¢£ŗ£ØĖ®¼Ū¼Ę·Ń![]() ×ŌĄ“Ė®ĻśŹŪ·ŃÓĆ
×ŌĄ“Ė®ĻśŹŪ·ŃÓĆ![]() ĪŪĖ®“¦Ąķ·ŃÓĆ£©
ĪŪĖ®“¦Ąķ·ŃÓĆ£©
×ŌĄ“Ė®ĻśŹŪ¼Ūøń | ĪŪĖ®“¦Ąķ¼Ūøń | |
Ć滧ĆæŌĀÓĆĖ®Įæ | µ„¼Ū£ŗŌŖ | µ„¼Ū£ŗŌŖ |
17¶Ö¼°ŅŌĻĀ |
| 0.80 |
³¬¹ż17¶Ö²»³¬¹ż30¶ÖµÄ²æ·Ö |
| 0.80 |
³¬¹ż30¶ÖµÄ²æ·Ö | 6.00 | 0.80 |
ĖµĆ÷£ŗ¢ŁĆ滧²śÉśµÄĪŪĖ®ĮæµČÓŚøĆ»§µÄÓĆĖ®Į棬¢ŚĖ®·Ń=×ŌĄ“Ė®·Ń+ĪŪĖ®“¦Ąķ·Ń£»
ŅŃÖŖŠ”Ć÷¼Ņ2013Äź3ŌĀ·ŻÓĆĖ®20¶Ö£¬½»Ė®·Ń66ŌŖ£»5ŌĀ·ŻÓĆĖ®25¶Ö£¬½»Ė®·Ń91ŌŖ£®
£Ø1£©Ēó![]() £¬
£¬![]() µÄÖµ£®
µÄÖµ£®
£Ø2£©Ėę×ÅĻÄĢģµÄµ½Ą“£¬ÓĆĖ®Į潫Ōö¼Ó”£ĪŖĮĖ½ŚŹ”æŖÖ§£¬Š”ĆĪ¼Ę»®°Ń6ŌĀ·ŻµÄĖ®·ŃæŲÖĘŌŚ²»³¬¹ż¼ŅĶ„ŌĀŹÕČėµÄ2%£¬ČōŠ”ĆĪ¼ÓµÄŌĀŹÕČėĪŖ9200ŌŖ£¬ŌņŠ”Ķõ¼Ņ6ŌĀ·Ż×ī¶ąÄÜÓĆĖ®¶ąÉŁ¶Ö£æ
”¾“š°ø”æ£Ø1£©a=2.2£¬b=4.2£»£Ø2£©ÕÅĄĻŹ¦¼ŅĮłŌĀ·Ż×ī¶ąÓĆĖ®40¶Ö£®
”¾½āĪö”æ
£Ø1£©øł¾Ż±ķøńŹÕ·Ń±ź×¼£¬¼°ÕÅĄĻŹ¦4”¢5Į½ŌĀÓĆĖ®Į攢Ė®·Ń£¬æÉµĆ³ö·½³Ģ×飬½ā³ö¼“æÉ£»
£Ø2£©ĻČÅŠ¶ĻÓĆĖ®Į泬¹ż30¶Ö£¬¼Ģ¶ųŌŁÓÉĖ®·Ń²»³¬¹ż184£¬æÉµĆ³ö²»µČŹ½£¬½ā³ö¼“æÉ£®
£Ø1£©ÓÉĢāŅā£¬µĆ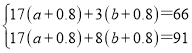 £¬
£¬
½āµĆ£ŗ![]() £®
£®
£Ø2£©µ±ÓĆĖ®ĮæĪŖ30¶ÖŹ±£¬Ė®·ŃĪŖ£ŗ17”Į2.2+13”Į4.2+0.8”Į30=116ŌŖ£¬9200”Į2%=184ŌŖ£¬
”ß116£¼184£¬
”ąÕÅĄĻŹ¦¼ŅĮłŌĀ·ŻµÄÓĆĖ®Į泬¹ż30¶Ö£¬
ÉčÕÅĄĻŹ¦¼Ņ6ŌĀ·ŻÓĆĖ®ĮæĪŖx¶Ö£¬
ÓÉĢāŅāµĆ£ŗ17”Į2.2+13”Į4.2+6£Øx-30£©+0.8x”Ü184£¬
½āµĆ£ŗx”Ü40£¬
”ąÕÅĄĻŹ¦¼ŅĮłŌĀ·Ż×ī¶ąÓĆĖ®40¶Ö£®


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
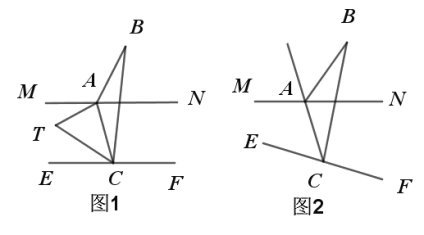
”¾ĢāÄæ”æŅŃÖŖµćAŗĶµćC·Ö±šŌŚÖ±ĻßMNŗĶÖ±ĻßEFÉĻ£¬µćBŌŚÖ±ĻßĶā£¬”ĻBAN=¦Į£¬”ĻBCF=¦Ā£®
£Ø1£©ČēĶ¼1£¬ČōMN”ĪEF£¬Ōņ”ĻB=””£ØÓƦĮ£¬¦ĀµÄŹ½×Ó±ķŹ¾£¬²»Š“Ö¤Ć÷¹ż³Ģ£©
£Ø2£©ŌŚ£Ø1£©µÄĢõ¼žĻĀ£¬µćTŌŚÖ±ĻßMNÓėÖ±ĻßEFÖ®¼ä£¬”ĻMAT=![]() ”ĻBAN£¬”ĻTCB=2”ĻTCE£¬Ēó”ĻBÓė”ĻTÖ®¼äµÄŹżĮæ¹ŲĻµ£®
”ĻBAN£¬”ĻTCB=2”ĻTCE£¬Ēó”ĻBÓė”ĻTÖ®¼äµÄŹżĮæ¹ŲĻµ£®
£Ø3£©ČēĶ¼2£¬ČōMN²»Ę½ŠŠÓŚEF£¬Ö±ĻßACĘ½·Ö”ĻMAB£¬ĒŅĘ½·Ö”ĻECB£¬Ōņ”ĻB=””£ØÓƦĮ£¬¦ĀµÄŹ½×Ó±ķŹ¾£¬²»Š“Ö¤Ć÷¹ż³Ģ£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬BDŹĒÕż·½ŠĪABCDµÄ¶Ō½ĒĻߣ¬BC=2£¬±ßBCŌŚĘäĖłŌŚµÄÖ±ĻßÉĻĘ½ŅĘ£¬½«ĶعżĘ½ŅʵƵ½µÄĻ߶Ī¼ĒĪŖPQ£¬Į¬½ÓPA”¢QD£¬²¢¹żµćQ×÷QO”ĶBD£¬“¹×ćĪŖO£¬Į¬½ÓOA”¢OP£®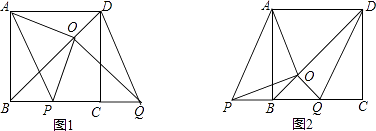
£Ø1£©ĒėÖ±½ÓŠ“³öĻ߶ĪBCŌŚĘ½ŅĘ¹ż³ĢÖŠ£¬ĖıߊĪAPQDŹĒŹ²Ć“ĖıߊĪ£æ
£Ø2£©ĒėÅŠ¶ĻOA”¢OPÖ®¼äµÄŹżĮæ¹ŲĻµŗĶĪ»ÖĆ¹ŲĻµ£¬²¢¼ÓŅŌÖ¤Ć÷£»
£Ø3£©ŌŚĘ½Ņʱ任¹ż³ĢÖŠ£¬Éčy=S”÷OPB £¬ BP=x£Ø0”Üx”Ü2£©£¬ĒóyÓėxÖ®¼äµÄŗÆŹż¹ŲĻµŹ½£¬²¢Ēó³öyµÄ×ī“óÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ņ»“ĪŗÆŹży=©x+4µÄĶ¼ĻóÓė·“±ČĄżŗÆŹży= ![]() £ØkĪŖ³£Źż£¬ĒŅk”Ł0£©µÄĶ¼Ļó½»ÓŚA£Ø1£¬a£©£¬BĮ½µć£®
£ØkĪŖ³£Źż£¬ĒŅk”Ł0£©µÄĶ¼Ļó½»ÓŚA£Ø1£¬a£©£¬BĮ½µć£®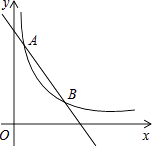
£Ø1£©Ē󷓱ȥżŗÆŹżµÄ±ķ“ļŹ½¼°µćBµÄ×ų±ź£»
£Ø2£©ŌŚxÖįÉĻÕŅŅ»µćP£¬Ź¹PA+PBµÄÖµ×īŠ”£¬ĒóĀś×ćĢõ¼žµÄµćPµÄ×ų±ź¼°”÷PABµÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCČżøö¶„µćµÄ×ų±ź·Ö±šĪŖA£Ø1£¬1£©£¬B£Ø4£¬2£©£¬C£Ø3£¬4£©.
(1) Ēė»³ö”÷ABCĻņ×óĘ½ŅĘ5øöµ„Ī»³¤¶ČŗóµĆµ½µÄ”÷A![]() B
B![]() C
C![]() £»
£»
(2) Ēė»³ö”÷ABC¹ŲÓŚŌµć¶Ō³ĘµÄ”÷A![]() B
B![]() C
C![]() £»
£»
(3) ŌŚ![]() ÖįÉĻĒó×÷Ņ»µćP£¬Ź¹”÷PABµÄÖܳ¤×īŠ”£¬Ēė»³ö”÷PAB£¬²¢Ö±½ÓŠ“³öPµÄ×ų±ź.
ÖįÉĻĒó×÷Ņ»µćP£¬Ź¹”÷PABµÄÖܳ¤×īŠ”£¬Ēė»³ö”÷PAB£¬²¢Ö±½ÓŠ“³öPµÄ×ų±ź.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĢ½Ė÷¹ęĀÉ£¬¹Ū²ģĻĀĆęÓÉ”ł×é³ÉµÄĶ¼°øŗĶĖćŹ½£¬²¢½ā“šĪŹĢā£®
1+3£½4£½22
1+3+5£½9£½32
1+3+5+7£½16£½42
1+3+5+7+9£½25£½52
£Ø1£©ŹŌŠ“³ö1+3+5+7+9+”+19£½”” ””£»
£Ø2£©ŹŌŠ“³ö1+3+5+7+9+”+£Ø2n©1£©£½”” ””£»
£Ø3£©ĒėÓĆÉĻŹö¹ęĀɼĘĖć£ŗ
¢Ł101+103+105+107+”+2017+2019£»
¢Ś£Ø2m+1£©+£Ø2m+3£©+£Ø2m+5£©+”+£Ø2n+7£©£ØĘäÖŠn£¾m£©£ØĮŠ³ö“śŹżŹ½¼“æÉ£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬½«”÷ABCÖ½Ę¬ŃŲDEÕŪµž£¬Ź¹µćAĀäŌŚµćA'“¦£¬ĒŅA'BĘ½·Ö”ĻABC£¬A'CĘ½·Ö”ĻACB£¬Čō”ĻBA'C=110”ć£¬Ōņ”Ļ1+”Ļ2µÄ¶ČŹżĪŖ£Ø””””£©

A. 80”ć£» B. 90”ć£» C. 100”ć£» D. 110”ć£»
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ņ»Å×ĪļĻߊĶ¹°ĒÅ£¬µ±¹°¶„µ½Ė®ĆęµÄ¾ąĄėĪŖ2Ć׏±£¬Ė®Ćęæķ¶ČĪŖ4Ć×£»ÄĒĆ“µ±Ė®Ī»ĻĀ½µ1Ć×ŗó£¬Ė®ĆęµÄæķ¶ČĪŖĆ×£® 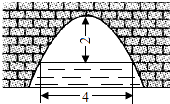
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßy=ax2+bx+c£Øa”¢b”¢cĪŖ³£Źż£¬a”Ł0£©¾¹żµćA£Ø©1£¬0£©£¬B£Ø5£¬©5£©£¬C£Ø6£¬0£©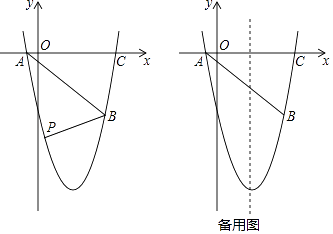
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©ČēĶ¼£¬ŌŚÖ±ĻßABĻĀ·½µÄÅ×ĪļĻßÉĻŹĒ·ń“ęŌŚµćPŹ¹ĖıߊĪPACBµÄĆ껿×ī“ó£æČō“ęŌŚ£¬ĒėĒó³öµćPµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
£Ø3£©ČōµćQĪŖÅ×ĪļĻߵĶŌ³ĘÖįÉĻµÄŅ»øö¶Æµć£¬ŹŌÖø³öŹ¹”÷QABĪŖµČŃüČż½ĒŠĪµÄµćQŅ»¹²ÓŠ¼øøö£æ²¢ĒėÄćĒó³öĘäÖŠŅ»øöµćQµÄ×ų±ź£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com