
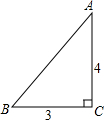
 如图,一张三角形纸片ABC,其中∠C=90°,AC=4,BC=3.现小林将纸片折叠:使点A落在B处.这折叠的折痕长$\frac{15}{8}$.
如图,一张三角形纸片ABC,其中∠C=90°,AC=4,BC=3.现小林将纸片折叠:使点A落在B处.这折叠的折痕长$\frac{15}{8}$. 分析 根据折叠得:GH是线段AB的垂直平分线,得出AG的长,再利用两角对应相等证△ACB∽△AGH,利用比例式可求GH的长,即折痕的长.
解答 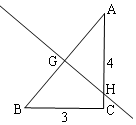 解:如图,折痕为GH,
解:如图,折痕为GH,
由勾股定理得:AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
由折叠得:AG=BG=$\frac{1}{2}$AB=$\frac{1}{2}$×5=$\frac{5}{2}$,GH⊥AB,
∴∠AGH=90°,
∵∠A=∠A,∠AGH=∠C=90°,
∴△ACB∽△AGH,
∴$\frac{AC}{AG}=\frac{BC}{GH}$,
∴$\frac{4}{\frac{5}{2}}$=$\frac{3}{GH}$,
∴GH=$\frac{15}{8}$,
故答案为$\frac{15}{8}$.
点评 本题考查了折叠的性质和相似三角形的性质和判定,折叠是一种对称变换,它属于轴对称,本题的关键是明确折痕是所折线段的垂直平分线,利用三角形相似来解决.


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:填空题
 为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边有总长为40m的栅栏围住,如图所示,若设绿化带的BC边长为xm,绿化带的面积为ym2,则y与y之间的函数表达式是y=$-\frac{1}{2}{x}^{2}$+20x,y取20时,y取得最大值是200.
为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一个矩形绿化带ABCD,绿化带一边靠墙,另三边有总长为40m的栅栏围住,如图所示,若设绿化带的BC边长为xm,绿化带的面积为ym2,则y与y之间的函数表达式是y=$-\frac{1}{2}{x}^{2}$+20x,y取20时,y取得最大值是200.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{{a}^{3}{b}^{2}}{{a}^{2}{b}^{3}}$=$\frac{a}{b}$ | B. | $\frac{(a-b)^{2}}{b-a}$=a-b | ||
| C. | $\frac{{m}^{2}-2m}{4-{m}^{2}}$=-$\frac{m}{m+2}$ | D. | $\frac{0.2a+b}{0.5a-b}$=$\frac{2a+10b}{5a-10b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
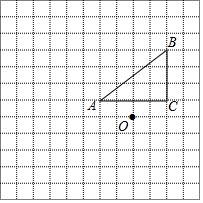 如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A、B、C都在格点上,将△ABC绕点A顺时针旋转90°,得到△AB′C′
如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点.△ABC的三个顶点A、B、C都在格点上,将△ABC绕点A顺时针旋转90°,得到△AB′C′查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com